Physics - Forces and Inertia

The previous page discussed momentum and how it is conserved in a closed system. This page is about how momentum can be exchanged between bodies by means of forces.

Not all forces transfer momentum, in some cases the forces may be in balance and therefore do not effect the dynamics. (see statics pages). If the forces are not in balance, then momentum will be transferred, this will create a force (inertia) which is equal and opposite to the sum of forces on the object.

In a collision between two objects the momentum can be exchanged very quickly (very large force in a very short time) in this case we call it an impulse as described here.

Newtons Second Law

A property of mass is its resistance to a change of velocity. This is quantified by Newtons second law which says that the acceleration is:

• Proportional to the net external force.
• Inversely proportional to its mass.
• In the direction of the force.

In other words:

F=m a

where:		other definitions
symbol	description	type	units
F	net force	vector	kg m/s2
m	mass	scalar	kg
a	acceleration	vector	m/s2

There is also an equivalent for rotation:

τa = [Ia]α or	in inertial fixed frame (varies with time)
τr = [Ir]α + ω×[Ir]ω	in body coordinates (inertia tensor fixed)

where:		other definitions
symbol	description	type	units
τa	torque in absolute coordinates (body being moved relative to ground)	bivector	N m
τr	torque in relative coordinates (control surfaces or jets on body)	bivector	N m
[Ia]	inertia tensor in absolute coordinates (this will vary with orientation and since the body is rotating the elements of the tensor will vary with time)	tensor	kg m2
[Ir]	inertia tensor in relative coordinates (since this is relative to the body it will be constant)	tensor	kg m2
α	angular acceleration	bivector	s-2

The first form of the equation looks simplest but the values vary with time and therefore the second form can be easier to use. Since it is, generally, very difficult to continuously recalculate the changing inertia matrix as seen from an inertial fixed frame, the conservation of angular momentum is most frequently written in a coordinate frame fixed in the rotating rigid body.

If the rotation vector is aligned with a principal axis of the rotating body then the term: ω×[I_r]ω becomes zero, the term: ω×[I_r]ω describes the behavior known as gyroscopic or processional motion.

Tensor - A set of components that obeys some transformation law in n-dimentional space. more

When working in 3 dimensions, then F, a, T and can be represented as vectors and m and I as matrices.

For example, then the equations become:

F=m a	Fx Fy Fz = m 0 0 0 m 0 0 0 m ax ay az
τ = [I] α	τx τy τz = ixx ixy ixz iyx iyy iyz izx izy izz αx αy αz

where x,y,z are the mutually perpendicular coordinate directions. Note that mass, m is the same in all directions whereas the coordinates of the inertia matrix depend on the orientation of the object and the individual elements represent the volume integrals as follows:

i_xx = ∫ ∫ ∫ (y² + z²) p dv
i_xy = - ∫ ∫ ∫ (x y) p dv
i_xz = - ∫ ∫ ∫ (x z) p dv
i_yx = - ∫ ∫ ∫ (y x) p dv
i_yy = ∫ ∫ ∫ (x² + z²) p dv
i_yz = - ∫ ∫ ∫ (y z) p dv
i_zx = - ∫ ∫ ∫ (z x) p dv
i_zy = - ∫ ∫ ∫ (z y) p dv
i_zz = ∫ ∫ ∫ (x² + y ²) p dv

6d vectors

So far the linear and angular components have been considered separately, however they are related, so it is useful to combine them. The method shown here uses the Featherstone's spatial vector notation (see http://www.syseng.anu.edu.au/~roy/technical.html) Thank you to Michael Shantz telling me about this (see hybridgdc.pdf file at http://michaelshantz.com ).

In this notation, the above equations are combined together as follows:

So when working in 3 dimensional space this can be expanded out to become the Newton-Euler equations of motion (since Newton originated the linear and Euler the angular).

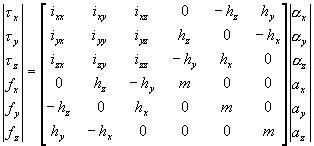
where:		other definitions
symbol	description	type	units
h	m * s = mass times distance	vector	Kg * m
τ	torque	bivector	Kg m2/s2
f	force	vector	Kg m/s2
α	angular acceleration	bivector	m-2
a	linear acceleration	vector	m/s2
i	inertia		Kg m2

The explanation for these h terms is because, when a solid object is rotating and contacts another object at a point offset from its axis of rotation, then linier forces can be converted into torques and visa versa.

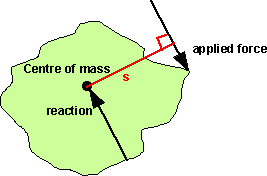
When a force is appled to a free floating rigid object, then an equal and opposite force is produced due to inertia. Since the two forces are offset by distance 's' then this will produce a turning moment.

This torque is equal to the force times its perpendicular distance from the centre of rotation.

τ = r × F

where:		other definitions
symbol	description	type	units
τ	torque	bivector	N m
r	distance from the centre of rotation	vector	m
F	the force	vector	N
×	the cross product vector operator

substituting F=m a (assuming m is constant) gives,

τ = r × m a

therefore defining h = m * gives

τ= h ×a

In the 3d case T, h and a are vectors and × is the cross product:

τx τy τz

=

0 -hz hy hz 0 -hx -hy hx 0

ax ay az

This give the h terms in the full matrix

EuclideanSpace

home

Screw Theory

Vector Cross Product

Bilinear and Quadratic Forms