Maths - Hyperbola and Parabola

Quadratic Equations in Two Variables

We can represent a general quadratic equation in two variables as:

A x² + B xy + C y²+ D x + E y + F = 0

In the same way that the quadratic equation in one variable:

a x² + b x + c = 0

has solutions

x=	-b ± √(b² - 4ac )
	2a

of different types depending whether:

b² - 4ac > 0	two real solutions
b² - 4ac = 0	one solution
b² - 4ac < 0	complex number solutions

So our quadratic equation in two variables has different types of solution.

circle	x² + y² = r²
ellipse	x² + y² =±1 a² b²
parabola	y² = 4 a x
hyperbola	x² - y² =±1 a² b²

These types can all be visualised as conic sections.

Equations of Hyperbola

east-west	north-south
x² - y² =1 a² b²	x² - y² = -1 a² b²
Parametric equations x = a cosh t y = b tanh t x = a/cos t y = b/tan t

For information about trig functions: cosh,tanh,cos,tan see this page.

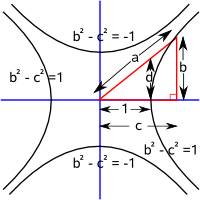
Hyperbola Focal Points

Equations of Parabola

y² = 4 a x

This can be represented by the intersection of the cone and a plane which is parallel to the face of the cone.

Equations of Circle and Ellipse

An ellipse is a circle that may be expanded differently in the x and y directions. Or, to reverse the argument, a circle is an ellipse whose extent is equal in both dimensions.

Circle	Ellipse
x² + y² = r²	x² + y² =±1 a² b²

When we intersect the cone with a plane parallel to its base we get a circle, when we intersect at an angle (But less than the angle of the cone face) then we get an ellipse.

Parametric equations

For comparison with above the parametric equations are:

x = a cosθ
y = b sinθ

Conic Sections

The equation for a cone in 3 dimensions is:

(x² + y²)cos²θ - z² sin²θ

Or in terms of parametric equations:

x = u cos(θ) cos(t)
y = u cos(θ) sin(t)
z = u sin(θ)

where:

• aperture =2θ

EuclideanSpace

home

Quadratic Equation

Projections