Here we will therefore investigate methods which start with very simple subsets of 'n' dimensional space;
- a point at the origin
- an infinite length line which goes through the origin
- an infinite plane which goes through the origin.
- in higher dimensions, we can extend this to hyperplanes which are like volumes in a higher number of dimensions
we can refer to these primitive subsets of space as flats and extend them in the following ways;
- associate the flats with a scalar quantity - directed length (line associated with a scalar quantity) directed area (plane associated with a scalar quantity -area).
- offset flats - modify the primitives so they are offset from the origin.
We can then combine these shapes with intersections and unions.
The advantage of this approach is that it has the same properties for any number of dimensions. This means we can embed a three dimensional space in a higher dimensional model which allows us to deal with rotational and transnational transforms in a linear way.So this subject is useful for fairly conventional 3D geometry, we will calculate projections, intersections and unions of these shapes. We can then go on to embed these elements in higher dimensional spaces, such as homogeneous and conformal space, this provides powerful ways to implement combined rotations and translations and also applications such as raytracing, this may eventually give us better ways to implement physics simulation.
Offset Elements
In the pages below this we define elements which go through the origin (Points, Lines, Planes, Volumes). We then add the ability to add an offset in such a way that it can be applied to any type of element, or it can be applied to a combination of elements together.
| element | D.O.F. of element in 3D | D.O.F. of offset in 3D | |
| Point | 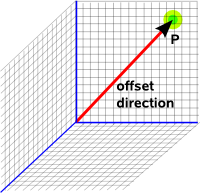 |
0 (point at origin can't move) | 3 |
| Line | 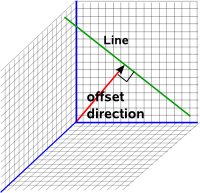 |
2 | 2 |
| Plane | 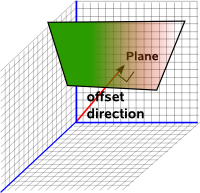 |
2 | 1 |
| Volume | whole space |
3 | 0 |
where:
- D.O.F. = degree of freedom (number of scalar values to specify)
Euclids Definitions.
Of course this is not new, for historical interest, here are Euclids Definitions.
- A point is that which has no part.
- A line is breadthless length.
- The extremities of a line are points.
- A straight line is a line which lies evenly with the points on itself.
- A surface is that which has length and breadth only.
- The extremities of a surface are lines.
- A plane surface is a surface which lies evenly with the straight lines on itself.
- A plane angle is the inclination to one another of two lines in a plane which meet one another and do not lie in a straight line.
- And when the lines containing the angle are straight, the angle is called rectilineal.
- When a straight line set up on a straight line makes the adjacent angles equal to one another, each of the equal angles is right, and the straight line standing on the other is called a perpendicular to that on which it stands.
- An obtuse angle is an angle greater than a right angle.
- An acute angle is an angle less than a right angle.
- A boundary is that which is an extremity of anything.
- A figure is that which is contained by any boundary or boundaries.
- A circle is a plane figure contained by one line such that all the straight lines falling upon it from one point among those lying within the figure are equal to one another;
- And the point is called the centre of the circle.
- A diameter of the circle is any straight line drawn through the centre and terminated in both directions by the circumference of the circle, and such a straight line also bisects the circle.
- A semicircle is the figure contained by the diameter and the circumference cut off by it. And the centre of the semicircle is the same as that of the circle.
- Rectilineal figures are those which are contained by straight lines, trilateral figures being those contained by three, quadrilateral those contained by four, and multilateral those contained by more than four straight lines.
- Of trilateral figures, an equilateral triangle is that which has its three sides equal, an isosceles triangle that which has two of its sides alone equal, and a scalene triangle that which has its three sides unequal.
- Further, of trilateral figures, a right-angled triangle is that which has a right angle, an obtuse-angled triangle that which has an obtuse angle, and an acute-angled triangle that which has its three angles acute.
- Of quadrilateral figures, a square is that which is both equilateral and right-angled; an oblong that which is right-angled but not equilateral; a rhombus that which is equilateral but not right-angled; and a rhomboid that which has its opposite sides and angles equal to one another but is neither equilateral nor right-angled. And let quadrilaterals other than these be called trapezia.
- Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction.
Postulates.
Let the following be postulated:
- To draw a straight line from any point to any point.
- To produce a finite straight line continuously in a straight line.
- To describe a circle with any centre and distance.
- That all right angles are equal to one another.
- That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.
Common Notions.
- Things which are equal to the same thing are also equal to one another.
- If equals be added to equals, the wholes are equal.
- If equals be subtracted from equals, the remainders are equal.
- [7]Things which coincide with one another are equal to one another.
- [8]The whole is greater than the part.

