Trigonometry is about angles and triangles, there are relationships between the angles and the ratios of the lengths of side of the triangles. These ratios are represented by functions such as sine and cosine, which occur widely in mathematics and physics, even in fields which don't initially appear to be related to physical triangles.
On these pages we will consider two types of trigonometry:
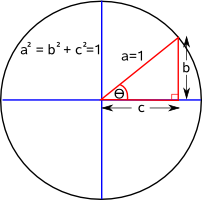
- trigonometry based on a circle where: a²=b²+c²
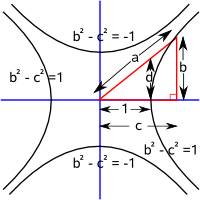
- trigonometry based on a hyperbola where: a²=b²-c²
For most cases we only need to consider traditional trigonometry based on a circle so feel free to ignore the hyperbolic trigonometry column. Hyperbolic trigonometry starts to become useful when we have a space with the Minkowski norm: (x²-y²) the simplest case is the two dimensional space represented by double numbers as explained here.
Summary of results
This is a summary of the results in the above pages, for the derivation of these formulae see the links above.
Right angled triangle
| circle based trigonometry | hyperbolic trigonometry |
|---|---|
| Here we will use a unit circle, that is a circle where all the points are exactly 1 unit from the origin, which gives: b²+c²=1. | Here we will use a hyperbolic function where the minimum distance from the origin is 1 unit which gives: b²-c²=±1. |
 |
 |
| sine function sin(θ) = b |
hyperbolic sine function |
| cosine function cos(θ) = c |
hyperbolic cosine function cosh(θ) = c |
| tangent function tan(θ) = b / c |
hyperbolic tangent function tanh(θ) = d = b/c |
| cosecant cosec(θ) = a / b |
|
| secant sec(θ) = a / c |
|
| cotangent cot(θ) = c / b |
Trig Identities
The values of sin, cos and tan are related to each other, for instance,
| circle based trigonometry | hyperbolic trigonometry |
|---|---|
| tan θ = sin θ / cos θ | tanh θ = sinh θ / cosh θ |
| cos2θ + sin2θ = 1 | cosh2θ - sinh2θ = 1 |
| cosec θ = 1 / sin θ | cosech θ = 1 / sinh θ |
| sec θ = 1 / cos θ | sech θ = 1 / cosh θ |
| cot θ = 1 / tan θ | coth θ = 1 / tanh θ |
hyperbolic
sinh(t) = (et - e-t )/2 = (et - 1)/2*et = -i sin(i t)
cosh(t) = (et + e-t )/2 = (et + 1)/2*et = cos(i t)
tanh(t) = (et - e-t )/(et + e-t ) = (e2t - 1)/(e2t + 1)= -i tan(i t)
asinh(x) = ln(x+√(x²+1))
acosh(x) = if (abs(x)<1) ln(x+√(1 - x²))
else
ln(x+√(x²-1))
atanh(x) = if (abs(x)<1) 0.5*ln((x-1)/(x+1))
else 0.5*ln((x-1)/(x+1))
Symmetric and Anti-symmetric Properties
| anti-symmetric | sin(θ)= -sin(-θ) | sinh(θ)= -sinh(-θ) | sin(iθ)= i sinh(θ) |
| symmetric | cos(θ)= cos(-θ) | cosh(θ)= cosh(-θ) | cos(iθ)= cosh(θ) |
| anti-symmetric | tan(θ)= -tan(-θ) | tanh(θ)= -tanh(-θ) | tan(iθ)= i tanh(θ) |
Complimentary and Supplementary Angles
- sin(θ - 90°) = cos(θ)
- cos(θ - 90°) = sin(θ)
- tan(θ - 90°) = cot(θ)
Non-Right Angled Triangles - The Sine Rule
a / sin A = b / sin B = c / sin C
Non-Right Angled Triangles - The Cosine Rule
- cos A = (b2 + c2 - a2)/2*b*c
- cos B = (c2 + a 2 - b 2)/2*c*a
- cos C = (a2 + b 2 - c 2)/2*a*b
Area of triangles
In euclidean space the area of a triangle depends on length of 2 sides and one angle:
area = 1/2 b * c*sin A
This is half the product of two sides and the sin of the included angle.
In hyperbolic space the area depends only on the internal angles:
π-(α+β+γ)=CΔ
Addition and Subtraction formulae
| circle based trigonometry | hyperbolic trigonometry |
|---|---|
| sin(A+B) = sin A cos B + cos A sin B | sinh(A+B) = sinh A cosh B + cosh A sinh B |
| cos(A+B) = cos A cos B - sin A sin B | cosh(A+B) = cosh A cosh B + sinh A sinh B |
tan(A+B) = (tan A + tan B)/ (1 - tan A tan B) |
tanh(A+B) = (tanh A + tanh B)/ (1 + tanh A tanh B) |
| sin(A-B) = sin A cos B - cos A sin B | sinh(A-B) = sinh A cosh B - cosh A sinh B |
| cos(A-B) = cos A cos B + sin A sin B | cosh(A-B) = cosh A cosh B - sinh A sinh B |
| tan(A-B) = (tan A - tan B)/ (1 + tan A tan B) |
tanh(A-B) = (tanh A - tanh B)/ (1 - tanh A tanh B) |
Products of Trigonometric Functions
| circle based trigonometry | hyperbolic trigonometry |
|---|---|
| sin A sin B = 0.5(cos(A-B)-cos(A+B)) | sinh A sinh B = 0.5(cosh(A+B)-cosh(A-B)) |
| cos A cos B = 0.5(cos(A-B)+cos(A+B)) | cosh A cosh B = 0.5(cosh(A+B)+cosh(A-B)) |
| sin A cos B = 0.5(sin(A-B)+sin(A+B)) | sinh A cosh B = 0.5(sinh(A+B)+sinh(A-B)) |
Double Angle and Half Angle Formulae
We can derive the double angle from products above where A=B. From this we can then derive the half angle formulae.
| circle based trigonometry | hyperbolic trigonometry |
|---|---|
| sin(2A) = 2 sin A cos A | sinh(2A) = 2 sinh A cosh A |
| cos(2A) = cos2A - sin2A = 1 - 2*sin2A | cosh(2A) = cosh2A + sinh2A |
| tan(2A) = 2 tan A/(1 - tan2A) | tanh(2A) = 2 tanh A/(1 + tanh2A) |
| sin(t/2) =±√(0.5 (1- cos(t))) | sinh(t/2) =±√(0.5 (cosh(t)-1)) |
| cos(t/2) =±√(0.5 (1+ cos(t))) | cosh(t/2) =±√(0.5 (1+ cosh(t))) |
| tan(t/2) = sin(t)/(1+cos(t)) | tanh(t/2) = sinh(t)/(1+cosh(t)) |
derivation on this page.
Angles of Any Magnitude
- sin(0) = 0
- cos(0) = 1
- cos(90° + θ) = -sin(θ)
- cos(90° - θ) = sin(θ)
- sin(180° - θ) = sin(θ)
- sin(180° + θ) = -sin(θ)
- sec(180° + θ) = -sec(θ)
- cosec(180° - θ) = cosec(θ)
- cos(270° + θ) = sin(θ)
- cos(270° - θ) =
- tan(270° + θ) = -cotan(θ)
- tan(270° - θ) = cotan(θ)
- cot(360° + θ) = cot(θ)
- sin(360° - θ) = -sin(θ)
Series
- sin(a) = a - ( a 3 / 3!) + ( a 5 / 5!) - ( a 7 / 7!) + ...
- cos(a) = 1 - ( a 2 / 2!) + ( a 4 / 4!) - ( a 6 / 6!) + ...
- tan(a) = a + ( a 3 / 3) + ( 2a5 / 15) + ...
- sin-1(x) = x + ( x3 / 3!) + ( 9x5 / 5!) + (225 x7 / 7!) + ...
- cos-1(x) = PI/2 - x - ( x3 / 3!) - (9 x5 / 5!) - ( 225 x7 / 7!) + ...
- tan-1(x) = x - ( x3 / 3) + ( x5 / 5) - ( x7 / 7) + ...
Other topics are as follows:
| triangles | relationships between sides and angles in triangles |
| trig functions | representing these relationships as continuous functions |
| pythagoras | relationship between length of sides of a right angle triangle |
| inverse trig functions | finding angle from ratio of sides arc sine, arc cosine, arc tan, etc. rectangular to polar conversion, need for atan2(y,x) function |
| derived functions | relationship between trig functions double angle formula |
| series | How to calculate the value of trig functions using an infinite series |
As a starting point goto this page: triangles

