A morphism between graphs is required to preserve structure, so,
A morpism between preordered sets is:
where:
|
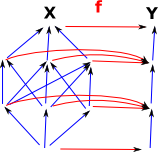 |
So a morphism between graphs maps nodes to nodes and edges to edges in a way the preserves the structure.
Decision Problem
Deciding if there is a morphism between graphs is an NP-complete problem. That is:
- It can be done in polynomial time.
- but there is no known efficient way to locate a solution.
Deciding if there is an isomorphism between graphs is also an important problem in computational complexity theory.
Hom Sets
We will use the notation:
Hom(A,X)
to denote all the possible morphisms from graph 'A' to graph 'X'.
Properties of Morphisms of Graphs
- If the output of one graph-morphism is the input to another graph-morphism then the morphisms can be composed to form another morphism.
- Graph morphism preserves connectedness.
- The tensor product of graphs is the category-theoretic product for the category of graphs and graph morphisms.
Graph Colourings
Graph colourings are an example of a graph-morphism where each node maps to a given colour.
Endomorphisms on Graphs

