Maths - Covectors

On the vector page we saw that vectors take elements with a field structure and create an array of these field elements which produces a vector space structure. This is described as a vector 'over' a field.

	name	operations	operands
combined structure	vector space	addition and scalar multiplication	scalar and vector
element structure	field	add,subtract, mult and divide	number such as integer, real and so on.

A covector is the dual of this:

• vector: field->vector space
• covector: vector space->field

that is: if we think of a vector as a mapping from a field to a vector space then a covector represents a mapping from a vector space to a field.

Contravarience

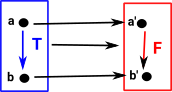
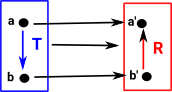
A 'functor' is a function which not only maps objects but it also maps operations (in this case transformations). These transformations must be consistent with the overall function, this can happen in two ways: covarience or contravarience:

Covarience		Contravarience
Here the transform F goes down (in the same direction as T)		Here the transform R goes up (in the opposite direction as T)

Covectors can be contravarient like this:

Imagine we have a point 'a', represented by a vector giving its position as an offset from the origin. This point is transformed by a matrix 'T' to the point 'b'. We can create a transform which goes in the reverse direction (from b to a) by mapping these points to a scalar value 's' (see 'representable functor'). This mapping from point to scalar can be represented by a covector.

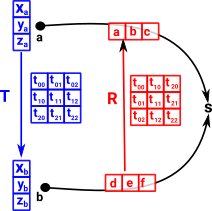We can choose some value for d,e,f to make 's' some value, say 3. So what value do we have to make a,b,c to give the same scalar value?

3 = d e f xb yb zb

We can just compose the arrows in the above diagram or substitute in the equation like this:

3 =

d e f

t00 t01 t02 t10 t11 t12 t20 t21 t22 xa ya za

So we have an arrow which goes from d,e,f to a,b,c so it is contravarient.

Linear Functional

So how can we construct a covector?

A linear function like:

ƒ(x,y,z) = 3*x + 4*y + 2*z

has similarities to vectors, for instance we can add them for instance if:

ƒ₁(x,y,z) = 3*x + 4*y + 2*z

and

ƒ₂(x,y,z) = 6*x +5*y + 3*z

then we can add them by adding corresponding terms:

ƒ₁(x,y,z) + ƒ₂(x,y,z) = 9*x + 9*y + 5*z

We can also apply scalar multipication, for instance:

2*ƒ₁(x,y,z) = 6*x + 8*y + 4*z

We can also multiply them together, for instance:

ƒ₁(x,y,z) * ƒ₂(x,y,z) = 18 x² + 39 xy + 20y² + 21 xz + 22 yz + 6z²

but this product is no longer linear but is quadratic.

So these functions have the same properties as vectors (that is they are isomorphic to vectors), however we now want to reverse this and make the functions ƒ₁and ƒ₂ the unknowns and the vector is the known:

	x		x		x		x
(a*ƒ1+ b*ƒ2+ c*ƒ3)(	y	)=(a*ƒ1)(	y	)+(b*ƒ2)(	y	)+(c*ƒ3)(	y	)
	z		z		z		z

So if we supply values for the vector what is the unknown function (or the function multipliers a,b and c) ?

3		7		8		4
4	=(	3	)+(b*ƒ2)(	4	)+(c*ƒ3)(	4	)
2		1		2		6

Duals

We can generalise this duality between vectors and covectors to tensors one of the aims of this type of approach is to analyze geometry and physics in a way that is independent of the coordinate system.

The duality shows itself in various ways :

1. If vectors are related to columns of a matrix then covectors are related to the rows.
2. The dot product of a vector and its corresponding covector gives a scalar.
3. When the coordinate system in changed then the covectors move in the opposite way to vectors (Contravariant and Covariant).
4. If a vector is made from a linear combination of basis vectors then a covector is made by combining the normals to planes.
5. When we take an infinitesimally small part of a manifold the vectors form the tangent space and the covectors form the cotangent space.
6. vector elements are represented by superscripts and covector elements are represented by subscripts.

Coordinate Independence

So lets start with a 3D global orthogonal coordinate system.

First we will start with a coordinate system based on a linear combination of orthogonal basis vectors.

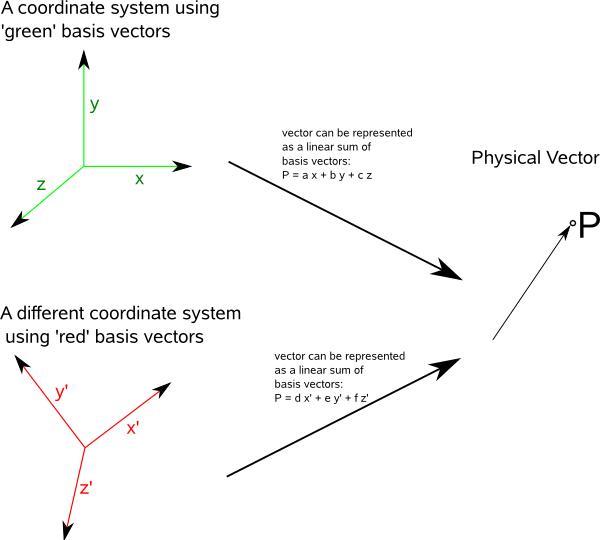
The physical vector 'p' can be represented by either:

p = ∑ v_ieⁱ in the red coordinate system and

p = ∑ v'_ie'ⁱ in the green coordinate system.

where:

• p = physical vector being represented in tensor terms
• v_i = tensor in the red coordinate system
• eⁱ= basis in the red coordinate system
• v'_i= tensor in the green coordinate system
• e'ⁱ = basis in the green coordinate system

So we can transform between the two using:

∑ v'^k = t^k_i v ⁱ

or

∑ e^k = t^'k_i e'ⁱ

where:

• t = a matrix tensor which rotates the vector v to vector '
• t' = a matrix tensor which rotates the basis e to the basis e'

Orthogonal Coordinates

We are considering the situation where a vector is measured as a linear combination of a number of basis vectors. We now add an additional condition that the basis vectors are mutually at 90° to each other. In this case we have:

e_i • e_j = δ_ij

where:

• e_i = a unit length basis vector
• e_j = another unit length basis vector perpendicular to the first.
• δ_ij= Kronecker Delta as described here.

If we choose a different set of basis vectors, but still perpendicular to each other, say e'_i and e'_j then we have:

e'_i • e'_j = δ_ij

To add more dimensions we can use:

e_ki • e_kj = δ_ij

This is derived from the above expression using the substitution property of the Kronecker Delta.

We could express the above in matrix notation:

e e^t= [I]

For example, in the simple two dimensional case:

e0 e1

e0 e1

=

e0•e0 e0•e1 e1•e0 e1•e1

=

1 0 0 1

since the basis vectors are orthogonal then:

e₀•e₀ = e₁•e₁ = 1
e₁•e₀ = e₀•e₁ = 0

also:

e^t e = 1

because:

e0 e1

e0 e1

=

e0•e0+e1•e1

=

1

but a scalar multiplication by 1 is the same as a matrix multiplication by [I] so we have: e^t e = e e^t= [I] = 1 = δ_ij

Now instead of looking at the basis vectors we will look at

a^T a = [I]

a0 a1

b0 b1

=

a0*b0 + a1*b1

where:

• a = a vector
• a^T= transpose of 'a'
• [I] = the identity matrix

We can combine these terminologies to give:

(a^T a)_ij = e_ki • e_kj = δ_ij

Any of these equations defines an orthogonal transformation.

Non-Orthogonal Coordinates

So far we assumed the coordinates are linear and orthogonal but what if the coordinates are curviliner?

 

EuclideanSpace

home

Prerequisites

You may want to review vectors:

• Vectors

Field

Directed Area

Duality