In geometry and mechanics a vector represents a magnitude and direction from the origin. In other subjects such as electrical engineering we can define equivalent definitions for vectors.
By using vector addition and subtraction we can use vectors to represent a magnitude and direction relative to some point other than the origin.
Vector operations (addition, subtraction and multiplication) can all be defined in a purely geometric way, for example, we can think of vector addition as moving the start of the second vector to the end of the first.
We can use vectors to represent points in space, however we need to be careful when doing this as some operations may apply differently to points and directions, so it is sometimes a good idea to maintain a distinction between points and magnitude/direction types of quantities.
Vectors also differ depending on whether we are operating in 2 dimensions, 3 dimensions, etc. A 2D vector is different from a 3D vector so we cant add vectors of different dimensions. Cross multiplication only applies to 3D vectors but otherwise different dimension vectors have similar properties.
Four, or more, dimensional vectors may not have such direct physical significance (although some physics theories may postulate higher numbers of dimensions) but they are still useful as we sometimes embed a model of our 3D world in a higher dimensional space to simplify the calculations.
Geometric Interpretation
A vector is a quantity with both magnitude and direction. Vectors have a different number of parameters depending on whether they are used in 2, 3 or more dimensions.
Displacements
In physical space vectors can represent displacements, that is the position of one point relative to another. This requires some cartesian (grid like) coordinate system. Related quantities such as velocities and accelerations can also be represented by vectors and so vectors can have units other than distance.
Points in space
Points in space can be represented by vectors as this is equivalent to a displacement relative to the origin of the coordinate system.
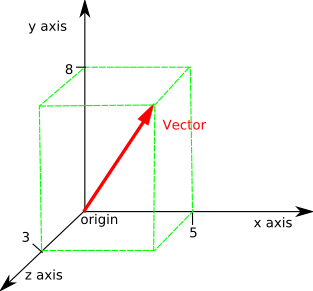
For example the vector shown above can represent the point (5,8,3)
Direction Only
We can use a vector to represent a direction only without a magnitude. An example might be when we want to specify the axis of a rotation. In this case we use a unit length vector. (see normalising)
Magnitude Only
The magnitude of a vector is a scalar quantity which can be easily calculated from the vector.
Bound Vector
Some quantities, such as force, have magnitude and direction and so can be specified by a vector. But to fully specify the force we need to define the point where it is acting and so we need two vectors to specify it fully.
Rays
Similar to the case above in that it needs two vectors to define it (see this page)
Representing Transformations
Can we use vector arithmetic to represent transformations such as reflections, rotations and translations?
| Translation | vp + vt where:
|
Reflection |
vp (vq•vq) - 2*vq (vq•vp) where:
|
Rotation (in 3D): |
-vp (vq•vq) + 2*vq (vq•vp) - sq*2*(vp x vq) + sq*sq*vp where:
|
The rotation equation only applies to rotations in 3 dimensions (the equation contains a cross multiplication).
Can anyone help me to derive the rotation equation from two reflections as described here?
The equation for rotation is quite complicated and it would be quite complicated to combine transformations using these equations. It is much easier to represent rotations using matrices or quaternions.
So I don't know if there is a practical application of these equations? Vector dot and cross multiplications occur often in physics and so it would be useful if we could use the same algebra for both.
Applications of Vectors
For 3D programming (the subject matter of this site) we are mainly concerned with vectors of 2 or 3 numbers.
A vector of dimension 3 can represent a physical quantity which is directional such as position, velocity , acceleration, force, momentum, etc.
For example if the vector represents a point in space, these 3 numbers represent the position in the x, y and z coordinates (see coordinate systems). Where x, y and z are mutually perpendicular axis in some agreed direction and units.
A 3 dimensional vector may also represent a displacement in space, such as a translation in some direction. In the case of the Java Vecmath library these are two classes: Point3f and Vector3f both derived from Tuple3f. (Note these use floating point numbers, there are also classes, ending in d, which contain double values). The Point3f class is used to represent absolute points and the Vector3f class represents displacement. In most cases the behavior of these classes is the same, as far as I know the difference between these classes is when they are transformed by a matrix Point3f will be translated by the matrix but Vector3f wont.
Here we are developing the following classes to hold a vector and encapsulate the operations described here,
It would be possible to build a vector class that could hold a vector of any dimension but a variable dimension class would be less efficient. Since we are concerned with objects in 3D space it is more important to handle 2D and 3D vectors efficiently.
Other vector quantities
Alternative interpretation of vectors
Upto now we have thought of the vector as the position on a 2,3 or n dimensional grid. However for some physical situations there may not be a ready defined Cartesian coordinate system. An alternative might be to represent the vector as a linear combination of 3 basis:
σ1
σ2
σ3
These basis don't have to be mutually perpendicular (although in most cases they probably will be) however they do have to be independent of each other, in other words they should not be parallel to each other and all 3 should not be in the same plane.
So a vector in 3 dimensions can be represented by [a,b,c] where a,b and c represent the scaling of the 3 basis to make the vector as follows:
a σ1 + b σ2 + c σ3
Note that if this vector represents position then it will be a relative position, i.e. relative to some other point, if we want to define an absolute point we still have to define an origin.
So the problem remains of how to define the basis, there may be some natural definition of these in the problem domain. Alternatively we could define the basis themselves as 3D vectors using a coordinate system. But why bother to do this, if we have a coordinate system why not just represent the vectors in this coordinate system? Well we might want to change coordinate systems or translate all the vectors in some way (see here). For example, we might want to represent points on a solid object in some local coordinate system, but the solid object may itself be moving relative to some absolute coordinate system.

