Finite Group Presentation to Permutation

Todd-Coxeter algorithm

In FriCAS the main group functionality is in PermutationGroup so it is useful to be able to convert to and from it. For conversions from presentations to PermutationGroup we use a well known algorithm called the Todd-Coxeter algorithm.

So a presentation consists of:

and each of these generators in the presentation will be a generator in the permutation, but it needs to be defined as a permutation, to do that we use the rules.

Each rule corresponds to a loop in the Cayley table so we need to use this to piece together a permutation for each generator. When we multiply together the permutations in each rule we get the identity permutation. We therefore work back from this to get the individual permutations for each generator.

The most efficient form of the algorithm is when we use subgroups, however just to keep things simple for the first example lets just concentrate on the basic method for now.

Example D3

In order to get some intuition lets look at the dihedral group of dimension 3. We will use 2 generators:

  • r - for rotate (modulo 3)
  • m - for mirror.
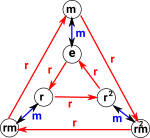 dihedral group

Then we get the following presentation and permutation:

presentation permutation
<r,m | rrr, mm, rmrm > r := (1,2,3)rotate m := (1,2)mirror

We can see how these two views interact by seeing what the rules do to permutations:

rrr mm rmrm
rotaterotaterotate mirrormirror rotatemirrorrotatemirror

As we can see each rule sends each point back to itself. This is to be expected because a rule corresponds to a loop in the Cayley table above.

FriCAS Code

Here is a simple version of the code without subgroups:

If you wish to see how the algorithm works (or does not work) try calling the function, with trace set to 'true', like this:

This will display the relatorTables at each stage and the deductions being made from the tables. 
(7) -> d3 := dihedralGroup(3)$GroupPresentation

   (7)  
                            Type: GroupPresentation
(8) -> toPermutationIfCan(d3,true)

   addPoint: cannot deduce more so adding a point
   adding:1 at row:1
                  +2  2  2+ +0  0+ +2  0  2  0+
   relatorTables=[|       |,|    |,|          |]
                  +0  0  0+ +0  0+ +0  0  0  0+
   addPoint: cannot deduce more so adding a point
   adding:2 at row:1
                  +2  2  2+ +3  3+ +2  3  2  3+
   relatorTables=[|0  0  0|,|0  0|,|0  0  0  0|]
                  +0  0  0+ +0  0+ +0  0  0  0+
   inferFromRelations found a gap of 1 so deduction made
   gap is in relator table:[2,2]
   distance from start:1 from end:0
   row at start:1
   row to change:3 new value:1
   generator index=2 invm=false
   forwardSequence:[1,3] backwardSequence:[1,0]
   inferFromRelations genIn=2 gb=1
                  +2  2  2+ +3  3+ +2  3  2  3+
   relatorTables=[|0  0  0|,|0  0|,|0  0  0  0|]
                  +0  0  0+ +1  1+ +0  1  0  1+
   addPoint: cannot deduce more so adding a point
   adding:1 at row:2
                  +2  2  2+ +3  3+ +2  3  2  3+
                  |4  4  4| |0  0| |4  0  4  0|
   relatorTables=[|       |,|    |,|          |]
                  |0  0  0| |1  1| |0  1  0  1|
                  +0  0  0+ +0  0+ +0  0  0  0+
   inferFromRelations found a gap of 1 so deduction made
   gap is in relator table:[1,1,1]
   distance from start:2 from end:0
   row at start:1
   row to change:4 new value:1
   generator index=1 invm=false
   forwardSequence:[1,2,4] backwardSequence:[1,0,0]
   inferFromRelations genIn=1 gb=2
                  +2  2  2+ +3  3+ +2  3  2  3+
                  |4  4  4| |0  0| |4  0  4  0|
   relatorTables=[|       |,|    |,|          |]
                  |0  0  0| |1  1| |0  1  0  1|
                  +1  1  1+ +0  0+ +1  0  1  0+
   addPoint: cannot deduce more so adding a point
   adding:2 at row:2
                  +2  2  2+ +3  3+ +2  3  2  3+
                  |4  4  4| |5  5| |4  5  4  5|
   relatorTables=[|0  0  0|,|1  1|,|0  1  0  1|]
                  |1  1  1| |0  0| |1  0  1  0|
                  +0  0  0+ +0  0+ +0  0  0  0+
   inferFromRelations found a gap of 1 so deduction made
   gap is in relator table:[2,2]
   distance from start:1 from end:0
   row at start:2
   row to change:5 new value:2
   generator index=2 invm=false
   forwardSequence:[2,5] backwardSequence:[2,0]
   inferFromRelations genIn=2 gb=1
                  +2  2  2+ +3  3+ +2  3  2  3+
                  |4  4  4| |5  5| |4  5  4  5|
   relatorTables=[|0  0  0|,|1  1|,|0  1  0  1|]
                  |1  1  1| |0  0| |1  0  1  0|
                  +0  0  0+ +2  2+ +0  2  0  2+
   inferFromRelations found a gap of 1 so deduction made
   gap is in relator table:[1,2,1,2]
   distance from start:2 from end:1
   row at start:1
   row to change:5 new value:3
   generator index=1 invm=false
   forwardSequence:[1,2,5,0] backwardSequence:[1,3,0,0]
   inferFromRelations genIn=1 gb=2
                  +2  2  2+ +3  3+ +2  3  2  3+
                  |4  4  4| |5  5| |4  5  4  5|
   relatorTables=[|0  0  0|,|1  1|,|0  1  0  1|]
                  |1  1  1| |0  0| |1  0  1  0|
                  +3  3  3+ +2  2+ +3  2  3  2+
   addPoint: cannot deduce more so adding a point
   adding:1 at row:3
                  +2  2  2+ +3  3+ +2  3  2  3+
                  |4  4  4| |5  5| |4  5  4  5|
                  |6  6  6| |1  1| |6  1  6  1|
   relatorTables=[|       |,|    |,|          |]
                  |1  1  1| |0  0| |1  0  1  0|
                  |3  3  3| |2  2| |3  2  3  2|
                  +0  0  0+ +0  0+ +0  0  0  0+
   inferFromRelations found a gap of 1 so deduction made
   gap is in relator table:[1,1,1]
   distance from start:1 from end:1
   row at start:3
   row to change:6 new value:5
   generator index=1 invm=false
   forwardSequence:[3,6,0] backwardSequence:[3,5,0]
   inferFromRelations genIn=1 gb=1
                  +2  2  2+ +3  3+ +2  3  2  3+
                  |4  4  4| |5  5| |4  5  4  5|
                  |6  6  6| |1  1| |6  1  6  1|
   relatorTables=[|       |,|    |,|          |]
                  |1  1  1| |0  0| |1  0  1  0|
                  |3  3  3| |2  2| |3  2  3  2|
                  +5  5  5+ +0  0+ +5  0  5  0+
   inferFromRelations found a gap of 1 so deduction made
   gap is in relator table:[1,2,1,2]
   distance from start:1 from end:2
   row at start:2
   row to change:4 new value:6
   generator index=2 invm=false
   forwardSequence:[2,4,0,0] backwardSequence:[2,5,6,0]
   inferFromRelations genIn=2 gb=1
                  +2  2  2+ +3  3+ +2  3  2  3+
                  |4  4  4| |5  5| |4  5  4  5|
                  |6  6  6| |1  1| |6  1  6  1|
   relatorTables=[|       |,|    |,|          |]
                  |1  1  1| |6  6| |1  6  1  6|
                  |3  3  3| |2  2| |3  2  3  2|
                  +5  5  5+ +0  0+ +5  0  5  0+
   inferFromRelations found a gap of 1 so deduction made
   gap is in relator table:[2,2]
   distance from start:1 from end:0
   row at start:4
   row to change:6 new value:4
   generator index=2 invm=false
   forwardSequence:[4,6] backwardSequence:[4,0]
   inferFromRelations genIn=2 gb=1
                  +2  2  2+ +3  3+ +2  3  2  3+
                  |4  4  4| |5  5| |4  5  4  5|
                  |6  6  6| |1  1| |6  1  6  1|
   relatorTables=[|       |,|    |,|          |]
                  |1  1  1| |6  6| |1  6  1  6|
                  |3  3  3| |2  2| |3  2  3  2|
                  +5  5  5+ +4  4+ +5  4  5  4+

   (8)  <(1 2 4)(3 6 5),(1 3)(2 5)(4 6)>
                    Type: Union(PermutationGroup(Integer),...)

Using Coset Tables

The above method so far is not very efficient because we just apply it to the whole group.

Now we want to use coset tables so that we can work with cosets rather than individual elements.

So again lets use our D3 example. We first want to work with coset tables such as stab(1) here:

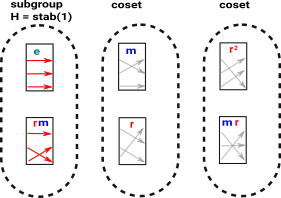stabiliser

Then we can work out the orbit+svc which will be:

[orb = [1,2,3], svc = [-1,1,2]]

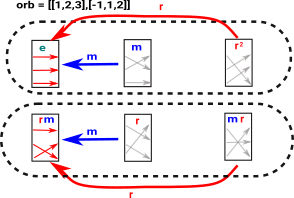 orbit

A coset table has a column for each generator element (and inverse generator element?) and a row for each coset.

Coset Table

Relator Table

for: mm

Relator Table

for: rrr

Relator Table

for: rmrm

  generators
cosets r m
   
   
   
  generators
cosets m m
1 2
   
   
  generators
cosets r r r
     
     
     
  generators
cosets r m r m
       
       
       

Spanning Tree

  generators
cosets                  
                 
                 
                 
                 
                 
                 
                 
                 

 

Further Work To Do

The conversions in both directions can be improved by implementing better simplifications but since there is no canonical form the simplifications can never be perfect. The Todd-Coxeter does not yet detect and remove 'coincidences', that is, duplicated points. So this in the next improvement that needs to be made.

Notes from Waldek

  
Subject: Re: [fricas-devel] [PATCH] add coerce from PermutationGroup to GroupPresentation
From: Waldek Hebisch
To: fricas-devel@googlegroups.com
Date: Wed, 25 Jan 2017 06:23:37 +0100 (CET)

Martin Baker wrote:
>
> I find it hard to understand the functions in PermutationGroup. Partly 
> because I cant find any documentation (I searched the usual places but 
> its easy to miss things) and its hard to follow the code because Rep is 
> so complicated.

Algorithm is described in A. Seress book "Permutation group algorithms",
but I do not think this book is freely available.  On the net
there are notes by A. Hulpke which contain sketch of the algorithm.

Data structure in a sense are very natural once you know what
algorithms are supposed to do.  More precisely, we have:

    Rep  := Record(gens : L PERM S, information : REC2)
    REC2 ==> Record(order : NNI, sgset : L V NNI, _
             gpbase : L NNI, orbs : V REC, mp : L S, wd : L L NNI)
    REC  ==> Record ( orb : L NNI, svc : V I )

in REP gens are original generators, information is extra
data coded in efficient form.  In particular, instead of
S internal computation works with integers: we first create
list of points appearing in all permutation and for internal
purposes we replace elements by position in the list.
Permutations are represented by vectors of integers, so
that v(i) gives image of point i.  Now in REC2 order is
number of elements in the group.  Value zero has special
meaning -- it means that no information is computed.
sgset is strong generators, gpbase is list of base points,
mp is list of elements of S moved by some permutation
(needed for mapping between permutations on S and
internal representation), wd gives representation of
strong generators in terms of orignal generators.
The most interesting structure is orbs which describes
orbits of base point.  The orb part is just list of
point on the orbit.  The svc part allows you to
compute element of the group moving given point to
base point of the orbit.  In detail, -2 means point
not in orbit, -1 means base point, positive value
is index of strong generator moving given point
closer to base point (look at 'strip' to see how
this is used).

Given that I know how presentation of permutation
group can be dane and that I know structure of
PermutationGroup I decide to code the convertion.
I need to do more test, but at least S5 seem to
work correctly.

I also noticed that Todd-Coxeter (toPermutationIfCan)
may produce something strange.  Namely, the following
(junky) relations:

   [[4,4,- 3,- 2,- 1,- 4,- 3], [3,4,- 2,- 4,- 3,- 2], [2,4,- 4,- 3,- 2],
    [1,4,- 4,- 3,- 1], [4,4,- 3,- 2,- 1,- 4,- 3,- 1], [3,4,- 2,- 4,- 3,- 1],
    [2,4,- 1,- 4,- 3], [1,4,- 4,- 3], [4,4,- 3,- 2,- 1,- 4,- 3,- 2],
    [3,4,- 1,- 2,- 1,- 4], [2,4,- 1,- 4,- 3,- 1], [1,4,- 1,- 4,- 3,- 2], [4,4],
    [3,4,- 4,- 3], [2,4,- 2,- 4], [1,4,- 1,- 4], [3,3,- 2,- 3,- 2],
    [2,3,- 3,- 2], [1,3,- 3,- 1], [3,3,- 2,- 3,- 1], [2,3,- 1,- 3], [1,3,- 3],
    [3,3,- 1,- 2,- 1], [2,3,- 1,- 3,- 1], [1,3,- 1,- 3,- 2], [2,2,- 1],
    [1,2,- 2], [2,2,- 1,- 2,- 1], [1,2,- 2,- 1], [1,1]]

and [1, 2, 3, 4] as generators produced set of permutations
on 6 elements which generates full symmetric group.  The
presentation above is junky because relation [1,2,- 2]
means that 1 is identity.  Then relation [2,2,- 1,- 2,- 1]
simplifies to [2,2,- 2] and next [2] which means that 2
is identity.  Then [3,3,- 2,- 3,- 1] means that 3 is
identity and [4,4,- 3,- 2,- 1,- 4,- 3] means 4 is
identity, so we get trivial group.

BTW: can you get smaller number of point than number of
elements in the group?  All correct examples I saw
produce just permutation representation on itself.
However, Todd-Coxeter in general produces representation
on cosets of a subgroup, so if you take notrivial
subgroup the set on which permutation act will be
smaller than the whole group.

-- 
                              Waldek Hebisch
  
I have now commited improved version of Todd-Coxeter.  It now
handles coincidencies and is much faster than previus version.
Scaling is not great, but much better than before: I was able
to do enumeration for Mathieu 11 (using second presentation from
Canon et all paper) in 211 seconds.

Currently coincidencies are handled using union-find and
table of equivalents.  It seems that we could handle them
more directly by careful updating of coset table.  But
that is potentially error-prone so I am using simpler
implementation now.

Coset with respect to a subgroup are still to do.

AFAICS still quite a lot of work goes into redundant
scanning of coset table.  We probably could get large
speedup by having some kind of agenda with current work,
so that after adding a point we could quickly
restart work waiting for this point.

-- 
                              Waldek Hebisch
  
Subject: [fricas-devel] Todd-Coxeter
To: fricas-devel@googlegroups.com
Date: Wed, 1 Feb 2017 17:33:40 +0100 (CET)
From: Waldek Hebisch

I looked more at Todd-Coxeter routine.  I think I now better
understand performance.  Basically Todd-Coxeter has tentative
set of coset starting from coset 1 and tries to apply relations
and perform inferences.  When same transition is undefined
in coset table we need to add new point.  Current routine
(in trunk) uses Felsch style strategy: we do all possible
inferences before adding a new point.  However, this repeats
a lot of work: if (partial) coset table is closed under
inferences than after adding a link any new inference must
involve added link.  So it is enough to try all relators
trough a link. In practice Felsch is starting all rotations
of relators and their inverses at one end of link.  One can
give simple estimate of running time for Felsch strategy
in terms of generators, relations and number of generated
cosets, number of operations is proportional to

M|G|\sum_i 2|r_i|^2

where M is number of generated cosets |G| is number of
generators and inverses, |r_i| is length of relator i.

Our implementation performs full scan of coset table
before adding a point so it is of order

M^2|G|\sum_i |r_i|

When M > max |r_i| our current code looses compared to
Felsch.  Actually, it is hard to imagine presentation for
which our current strategy would work better than Felsch:
Felsch has extra cost due to square of relator lengths,
So one would have to use long relators such that we
get small number of cosets -- looks weird.

There is different strategy: Haselgrove-Leech-Trotter
(HLT) method tries to complete relators trough given point
adding new point if necessary.  Because it adds point
early it may add point which later will be proven to
be equal to already added point.  So for given order
of adding point HLT will need the same or larger
number of point than Felsch.  But HLT saves work
on perfroming inferences: we apply given relator
(or invere) to given coset only once.  So one
can  give simple estimate of number of operations:

M|G|\sum_i |r_i|

where M is number of generated cosets |G| is number of
generators and inverses, |r_i| is length of relator i.
Since HLT may generate more cosets there is a tradeoff.

I have now implemented HLT type strategy.  It is worse,
because after adding point I come back to applying all
relators to the coset.  For m11 result is good (about
120 ms) in other not so.  Anyway some results are:

Current (trunk with small improvenents):

m11 w 182.19 using 14830 cosets

HLT style:

m11 w 0.12 sec using 47966 cosets
a5 from relationsInGenerators 0.01 sec using 678 cosets
a6 from relationsInGenerators 2.62 sec using 35831 cosets
s5 from relationsInGenerators 0.63 sec using 10692 cosets
s6 from relationsInGenerators after long time run out of stack space ...

As you can see relationsInGenerators seem to produce bad
(expensive to enumenrate) presentations.

You can see the HLT thing at:

http://www.math.uni.wroc.pl/~hebisch/fricas/gpresent.spad

I reused location of previous version so click reload in
brewser to get fresh one.

TODO:
- real HLT (without rescanning coset from the beginning),
  should get rid of quadratic behaviour for long relators
- real Felsch (probably need to keep relators in array to
  have easy access to rotated version).
- get rid of find and reuse entries in coset table.

I will do few more test with this version.  Early tests
discoverd bug in handling coincidencies and I could do
m11 only after fixing this bug.  If all goes well I
will commit this or better version soon.

-- 
                              Waldek Hebisch

 

metadata block
see also:
Correspondence about this page

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.