Example D3
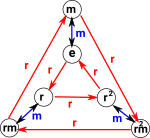
In order to get some intuition lets look at the dihedral group of dimension 3. This has 2 generators:
|
 |
Then we get the following presentation and permutation:
| presentation | permutation | |
|---|---|---|
| <r,m | rrr, mm, rmrm > | r := (1,2,3) |
m := (1,2) |
We can see how these two views interact by seeing what the rules do to permutations:
| rrr | mm | rmrm |
|---|---|---|
As we can see each rule sends each point back to itself. This is to be expected because a rule corresponds to a loop in the Cayley table above.
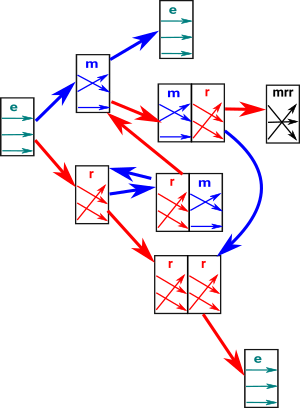
So how do we derive a presentation from the permutation? We already gan get the generators from the existing permgrps.spad code. So the problem is to work out the rules.
My first thought is that each rule corresponds to the loops in the Cayley graph (above). A brute force way to get all the loops is to start at 'e' and keep applying generators in a tree structure until we get back to 'e', the each of these paths from 'e' back to 'e' is a loop.
Examples
(1) -> )expose PermutationGroupExamples
PermutationGroupExamples is now explicitly exposed in frame frame1
(1) -> d3 := dihedralGroup(3)$PermutationGroupExamples
(1) <(1 2 3),(1 3)>
Type: PermutationGroup(Integer)
(2) -> initializeGroupForWordProblem(d3)
Type: Void
(3) -> sg := strongGenerators(d3)
(3) [(2 3),(1 3)]
Type: List(Permutation(Integer))
(4) -> b := base(d3)
(4) [1,2]
Type: List(Integer) |
From: Martin Baker
Subject: [PATCH] add coerce from PermutationGroup to GroupPresentation
Organization: axiom
Date: Mon, 14 Nov 2016 18:08:13 +0000
Patch is here:
https://github.com/martinbaker/fricasAlgTop/blob/master/permgrps1.patch
File is here:
https://github.com/martinbaker/fricasAlgTop/blob/master/permgrps.spad
It is used like this:
permgp := dihedralGroup(3)$PermutationGroupExamples
(1) <(1 2 3),(1 3)>
Type: PermutationGroup(Integer)
permgp::GroupPresentation
(2)
<ha b |
a*a*a, a*a*b*a*a*b, a*a*b*a*a*-b, a*b*a*b, a*b*a*-b, b*b,
a*a*b*-a*b
,
a*b*-a*-a*b, b*a*a*-b*-a, a*a*b*-a*-b, a*a*-b*a*a*-b, a*-b*a*-b
>
Type: GroupPresentation
As discussed before, improvements to simplification in GroupPresentation
would be good but that is not part of this code.
Martin B |
Subject: Re: [fricas-devel] [PATCH] add coerce from
PermutationGroup to GroupPresentation
From: Waldek Hebisch
To: fricas-devel@googlegroups.com
Date: Mon, 23 Jan 2017 06:37:51 +0100 (CET)
Martin Baker wrote:
>
> Patch is here:
> https://github.com/martinbaker/fricasAlgTop/blob/master/permgrps1.patch
I have tried it now. AFAICS it is _extremally_ inefficient:
coerce(symmetricGroup(4))@GroupPresentation crashes due to
running out of memory (tested on sbcl with default 1GB limit),
coerce(dihedralGroup(7))@GroupPresentation works but takes
a lot of time and produces large presentation.
Very naive and inefficient way to produce group presentation
is to first produce a word for each group element and then
for each pair (g,w) where g i a generator and w is an
element to produce relation gw = z where z is word representing
gw (since we have word for each element we can find it via
lookup). Clearly, denoting by n number of generators and
by N number of group elements this methods needs nN multiplications
and will produce nN relations. This should work well
when nN is of order several thousend.
AFAICS you try something similar, but there is something
wrong with your method because it cannot handle _very_
small groups. Little remark: you use both generators and
inverses. This may give shorter words, so there may be
useful for representing group elements. However relations
obtained from inverses are redundant: inverse a power
of generator so once we have relations for gw relations
for inverses are a conseqence.
The main routine in PERMGRP computes base and strong generating
set for the group. Effectively, this means that we
have sequence of generators g_ik and groups G_i such that
G_i = <g_ik, G_{i+1}> and
G_0 = G and
G_i for i>0 is
stabilizer of point b_i (set of b_i-s is called a base
and g_ik are called strong generators).
In terms of stong generators one can recursively build
presentation. More precisely, given presentation for G_{i+i}
we can build presentation for G_i in the following way.
Let S_i be G_ib_i (that is G_i-orbit of b_i).
For each s in S w fix a word w_s in terms of strong generators
such that w_sb_i = s.
Each element of G_i can be written as
w_sz with z in G_{i+1}.
Namely, if x is
an arbitrary element of G_i, and s = xb_i then
((w_s)^{-1}x)(b_i) = b_i, so z = (w_s)^{-1}x in G_{i+1}
and x = w_sg. We call w_sz canonical word for x
(more precisely we should recursively find canonical
word for z in G_{i+1}). Now, relations for G_i are
relations for G_{i+1} plus new relations of form
gw_s = w_tz where g runs over (stong) generators of G_i
and w_tz is canonical word corresponding to gw_s.
This is presentation for G_i because:
- for each element of G_i we have a canonical word
- each word is eqivalent to a canonical word
(proved by induction: by our choice of relations
gw_sz_1 is equivalent to w_tz_2z_1 and by assumption
about G_{i+1} z_2z_1 is equivalent to canonical
word z_3
- action of free group F_i on strong generators of G_i
acting on canonical words via multiplication from left
and reduction to canonical form agrees with natural action
of F_i on G_i
The first two point means that we can identify as a set
resulting finitely presented group with G_i. The third
one means that group actions coincide.
Once we have presentation in terms of strong generators
we can produce also presentation in terms of original
generators. The trick is that first we express each
strong generator in terms of original generators.
Then we rewrite each relation using fixed correspondence
from the first step. Finally for each original generator
h and each strong generator g we add relation hg = z
where z is word representing hg in terms of strong
generators rewritten in terms of original generators
using fixed relation from first step. As before,
for each element of G we get a canonical word. Again
we can rewrite any word in terms of original generators
to a canonical word and we can prove that multiplication
on canonical words agrees with multiplication in G.
Obtained presentations are likely to be quite large,
but AFAICS size of presentation will be similar
to cost of producing strong generating set. So
we should be able to handle groups having more
than 10^20 elements, which is clearly beyond
what naive method could do.
--
Waldek Hebisch |
From: Waldek Hebisch
Subject: Re: [fricas-devel] [PATCH] add coerce
from PermutationGroup to GroupPresentation
To: fricas-devel@googlegroups.com
Date: Mon, 23 Jan 2017 17:58:32 +0100 (CET)
A little example of using strong generators:
(1) -> s5 := symmetricGroup(5)$PGE
(1) <(1 2 3 4 5),(1 2)>
Type: PermutationGroup(Integer)
(2) -> initializeGroupForWordProblem(s5)
Type: Void
(3) -> strongGenerators(s5)
(3) [(4 5),(3 4 5),(2 5 3),(1 2)]
Type: List(Permutation(Integer))
(4) -> base(s5)
(4) [1,2,3,4]
Type: List(Integer)
So we have:
G = G_0 = <(1,2), G_1>,
G_1 = <(2,5,3), G_2>,
G_2 = <(3,4,5), G_3>,
G_3 = <(4,5)>.
Writing
a = (1,2),
b = (2,5,3),
c = (3,4,5),
d = (4,5)
we get the following relations:
for G_3: base point 4, orbit is {4, 5},
single generator d and single relation d^2
for G_2: base point is 3, orbit is {3, 4, 5},
single generator c produces the orbit:
3 = c^0(3), 4 = c(3), 5 = c^2(3),
c^3(3) = 3 and we get relation c^3
dc(3) = 5 so dc = c^2d. We need no
extra relation for product of d and c^2
as this follows from relation for dc:
dc^2 = (dc)c = c^2dc = c^2c^2d = cd
for G_1: base point 2, orbit is {2, 3, 4, 5}
we need two generators to produce the
orbit: b(2) = 5, b^2(2) = 3, db(2) = 4.
We get relation b^3, cb(2) = 3 so
cb = b^2dcd, cb^2(2) = 4 so cb^2 = dbdc,
since d^2 = e we have d^2b = b
and need no extra relation for product of
d and db, cdb(2) = 5 so cdb = bd, bdb(2) = 4
so bdb = dbc
for G_0: base point is 1, orbit is {1, 2, 3, 4, 5},
we need 3 generators to get orbit:
a(1) = 2, ba(1) = 5, b^2a(1) = 3, dba(1) = 4.
We get relation a^2, aba(1) = 5 so aba = ba*dcb,
ab^2a(1) = 3, so ab^2a = b^2acdbc, adba(1) = 4
so adba = dba*dcb, for product of b and a
we need no extra relation as ba is already
canonical, similarly for product of b and ba,
for product of b and b^2a we need no extra
relation because b^3a = a by relation b^3,
bdba(1) = 4 so bdba = dbac. In similar
way we get relations ca = ac, cba = b^2adcd,
cb^2a = dbadc, cdba = bad, da = ad, db^2a = b^2acd,
(for dba we need no extra relation because it
is canonical, for d(dba) from d^2 = e we get ddba = ba).
Together we get generators a, b, c, d and relations:
d^2 = e,
c^3 = e,
dc = c^2d,
b^3 = e,
cb = b^2dcd,
cb^2 = dbdc,
bdb = dbc,
a^2 = e,
aba = badcb,
ab^2a = b^2acdbc,
adba = dbadcb,
bdba = dbac,
ca = ac,
cba = b^2adcd,
cb^2a = dbadc,
cdba = bad,
da = ad,
db^2a = b^2acd.
Note: I used wordInStrongGenerators as a helper, but part of
calculation is by hand so there may be mistakes. However,
it should be clear that method scales to much larger groups
and already in this case presentation is smaller than obtained
by naive algorithm. I skip expressing relations in terms
of original generators, but for this we would get 8 extra
relations so this still will have smaller number of relations
than naive algorithm gives (admitedly, the relations would
be quite long).
--
Waldek Hebisch
|
From: Martin Baker
Subject: Re: [fricas-devel] [PATCH] add coerce from
PermutationGroup to GroupPresentation
To: fricas-devel@googlegroups.com
Date: Mon, 23 Jan 2017 16:59:01 +0000
On 01/23/2017 05:37 AM, Waldek Hebisch wrote:
> Martin Baker wrote:
>> Patch is here:
>> https://github.com/martinbaker/fricasAlgTop/blob/master/permgrps1.patch
> I have tried it now. AFAICS it is _extremally_ inefficient:
> coerce(symmetricGroup(4))@GroupPresentation crashes due to
> running out of memory (tested on sbcl with default 1GB limit),
> coerce(dihedralGroup(7))@GroupPresentation works but takes
> a lot of time and produces large presentation.
Waldek,
Thank you for looking at this. I did not find a published algorithm for
this so I just worked out a simple algorithm myself, I did not think
much about efficiency I was just happy to hit on a method that worked.
The main issue is finding the relations. It seems to me that each
relation corresponds to a loop in the Cayley graph.
So I just wrote an algorithm that found all the relations (loops) by
doing a tree search of the Cayley graph. Obviously this finds a lot of
redundant rules (loops).
Am I correct in thinking that the algorithm that you are proposing is
more efficient because it uses a stabilizer chain (sequence of
subgroups, each containing the next and each stabilizing one more
point). So when we work out the loops in the subgroup we implicitly
encode information about the loops in the cosets so we consider less loops?
Martin B |
Subject: Re: [fricas-devel] [PATCH] add coerce from
PermutationGroup to GroupPresentation
To: fricas-devel@googlegroups.com
From: Martin Baker
Date: Mon, 23 Jan 2017 17:13:06 +0000
On 01/23/2017 04:58 PM, Waldek Hebisch wrote:
> Note: I used wordInStrongGenerators as a helper
I find it hard to understand the functions in PermutationGroup. Partly
because I cant find any documentation (I searched the usual places but
its easy to miss things) and its hard to follow the code because Rep is
so complicated.
For example, how does wordInGenerators work? I sort of expected that the
generators would be represented by a single element in the word. So I
expected that the following would give [[1],[2]]:
dg3 := dihedralGroup(3)
(1) <(1 2 3),(1 3)>
Type: PermutationGroup(Integer)
g := generators(dg3)
(2) [(1 2 3),(1 3)]
Type: List(Permutation(Integer))
[wordInGenerators(x,dg3) for x in g]
(3) [[1,2,2],[2]]
Type: List(List(NonNegativeInteger))
I realise this is the same as [[1],[2]] because 2 is self inverse but it
would be good if it could do some simplification.
wordsForStrongGenerators is different from wordInGenerators in that it
does not seem to use indexes.
sg := strongGenerators(dg3)
(4) [(2 3),(1 3)]
Type: List(Permutation(Integer))
w := wordsForStrongGenerators(dg3)
(5) [[1,2],[2]]
Type: List(List(NonNegativeInteger))
Now that I have your example hopefully I will now be able to understand
it better.
Thanks,
Martin |
Subject: Re: [fricas-devel] [PATCH] add coerce from
PermutationGroup to GroupPresentation
From: Waldek Hebisch
To: fricas-devel@googlegroups.com
Date: Mon, 23 Jan 2017 18:13:40 +0100 (CET)
Martin Baker wrote:
>
> On 01/23/2017 05:37 AM, Waldek Hebisch wrote:
> > Martin Baker wrote:
> >> Patch is here:
> >> https://github.com/martinbaker/fricasAlgTop/blob/master/permgrps1.patch
> > I have tried it now. AFAICS it is _extremally_ inefficient:
> > coerce(symmetricGroup(4))@GroupPresentation crashes due to
> > running out of memory (tested on sbcl with default 1GB limit),
> > coerce(dihedralGroup(7))@GroupPresentation works but takes
> > a lot of time and produces large presentation.
>
> Waldek,
>
> Thank you for looking at this. I did not find a published algorithm for
> this so I just worked out a simple algorithm myself, I did not think
> much about efficiency I was just happy to hit on a method that worked.
>
> The main issue is finding the relations. It seems to me that each
> relation corresponds to a loop in the Cayley graph.
Yes.
> So I just wrote an algorithm that found all the relations (loops) by
> doing a tree search of the Cayley graph. Obviously this finds a lot of
> redundant rules (loops).
>
> Am I correct in thinking that the algorithm that you are proposing is
> more efficient because it uses a stabilizer chain (sequence of
> subgroups, each containing the next and each stabilizing one more
> point). So when we work out the loops in the subgroup we implicitly
> encode information about the loops in the cosets so we consider less loops?
Yes. Within coset we get a lot of implied relations (loops). We
only need to add a single loop for each pair (generator, coset representative).
In fact, for some pairs (generator, coset representative) we need
no relation as in example from another message.
--
Waldek Hebisch |
Subject: Re: [fricas-devel] [PATCH] add coerce from
PermutationGroup to GroupPresentation
From: Waldek Hebisch
To: fricas-devel@googlegroups.com
Date: Mon, 23 Jan 2017 18:22:33 +0100 (CET)
Martin Baker wrote:
>
> On 01/23/2017 04:58 PM, Waldek Hebisch wrote:
> > Note: I used wordInStrongGenerators as a helper
>
> I find it hard to understand the functions in PermutationGroup. Partly
> because I cant find any documentation (I searched the usual places but
> its easy to miss things) and its hard to follow the code because Rep is
> so complicated.
>
> For example, how does wordInGenerators work?
It first writes word in terms of strong generators and then
rewrites strong generators in terms of generators.
> I sort of expected that the
> generators would be represented by a single element in the word. So I
> expected that the following would give [[1],[2]]:
>
> dg3 := dihedralGroup(3)
>
> (1) <(1 2 3),(1 3)>
> Type: PermutationGroup(Integer)
> g := generators(dg3)
>
> (2) [(1 2 3),(1 3)]
> Type: List(Permutation(Integer))
> [wordInGenerators(x,dg3) for x in g]
>
> (3) [[1,2,2],[2]]
> Type: List(List(NonNegativeInteger))
>
> I realise this is the same as [[1],[2]] because 2 is self inverse but it
> would be good if it could do some simplification.
I would have to check if there are some simplifications. But
basically, there is no efficient algorithm to directly work
with original generators, so all is done in terms of strong
generators and (if requested) rewritten later.
> wordsForStrongGenerators is different from wordInGenerators in that it
> does not seem to use indexes.
>
It uses indexes. Note that 'wordsForStrongGenerators' and
'wordInStrongGenerators' are different functions.
--
Waldek Hebisch |