The main Axiom/FriCAS code for working with groups is PermutationGroup, this is good for working with large groups, however I wanted a complimentary domain defined in terms of the Cayley table which can represent groups and semigroups, support cosets and so on.
PermutationGroup is derived from SetCategory rather than group because of the way that it uses Permutation as elements.
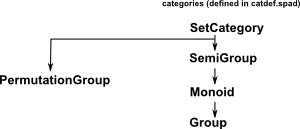
What I would like to do is add additional group related domains defined by a group table:
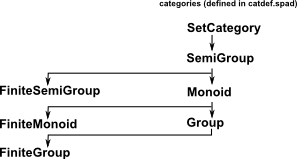
Example
This is how I am using this code to add to the capability of the existing domains (for more explanation see this page):
d1 := dihedralGroup(1)
<(1 2)>
Type: PermutationGroup(Integer)
toTable()$toFiniteGroup(d1,1)
Type: Table(2)
permutationRepresentation(d1,2)
Type: List(Matrix(Integer))
d2 := dihedralGroup(2)
<(1 2), (3 4)>
Type: PermutationGroup(Integer)
toTable()$toFiniteGroup(d2,1)
| i |
a |
b |
ab |
| a |
i |
ab |
b |
| b |
ab |
i |
a |
| ab |
b |
a |
i |
Type: Table(4)
permutationRepresentation(d2,2)
Type: List(Matrix(Integer))
d3 := dihedralGroup(3)
<(1 2 3),(1 3) >
Type: PermutationGroup(Integer)
toTable()$toFiniteGroup(d3,1)
| i |
a |
b |
aa |
ab |
ba |
| a |
aa |
ab |
i |
ba |
b |
| b |
ba |
i |
ab |
aa |
a |
| aa |
i |
ba |
a |
b |
ab |
| ab |
b |
a |
ba |
i |
aa |
| ba |
ab |
aa |
b |
a |
i |
Type: Table(6)
permutationRepresentation(d3,3)
Type: List(Matrix(Integer))
d4 := dihedralGroup(4)
< (1 2 3 4 ), (1 4)(2 3)>
Type: PermutationGroup(Integer)
toTable()$toFiniteGroup(d4,1)
| i |
a |
b |
aa |
ab |
ba |
aaa |
aab |
| a |
aa |
ab |
aaa |
aab |
b |
i |
ba |
| b |
ba |
i |
aab |
aaa |
a |
ab |
aa |
| aa |
aaa |
aab |
i |
ba |
ab |
a |
b |
| ab |
b |
a |
ba |
i |
aa |
aab |
aaa |
| ba |
aab |
aaa |
ab |
aa |
i |
b |
a |
| aaa |
i |
ba |
a |
b |
aab |
aa |
ab |
| aab |
ab |
aa |
b |
a |
aaa |
ba |
i |
Type: Table(8)
permutationRepresentation(d4,4)
| [ |
| 0 |
0 |
0 |
1 |
| 1 |
0 |
0 |
0 |
| 0 |
1 |
0 |
0 |
| 0 |
0 |
1 |
0 |
|
, |
| 0 |
0 |
0 |
1 |
| 0 |
0 |
1 |
0 |
| 0 |
1 |
0 |
0 |
| 1 |
0 |
0 |
0 |
|
|
] |
Type: List(Matrix(Integer))
d5 := dihedralGroup(5)
<(1 2 3 4 5) , ( 1 5) (2 4 )>
Type: PermutationGroup(Integer)
toTable()$toFiniteGroup(d5,1)
| i |
a |
b |
aa |
ab |
ba |
aaa |
aab |
baa |
bab |
| a |
aa |
ab |
aaa |
aab |
b |
bab |
baa |
ba |
i |
| b |
ba |
i |
baa |
bab |
a |
aab |
aaa |
aa |
ab |
| aa |
aaa |
aab |
bab |
baa |
ab |
i |
ba |
b |
a |
| ab |
b |
a |
ba |
i |
aa |
baa |
bab |
aaa |
aab |
| ba |
baa |
bab |
aab |
aaa |
i |
ab |
aa |
a |
b |
| aaa |
bab |
baa |
i |
ba |
aab |
a |
b |
ab |
aa |
| aab |
ab |
aa |
b |
a |
aaa |
ba |
i |
bab |
baa |
| baa |
aab |
aaa |
ab |
aa |
bab |
b |
a |
i |
ba |
| bab |
i |
ba |
a |
b |
baa |
aa |
ab |
aab |
aaa |
Type: Table(10)
permutationRepresentation(d5,5)
| [ |
| 0 |
0 |
0 |
0 |
1 |
| 1 |
0 |
0 |
0 |
0 |
| 0 |
1 |
0 |
0 |
0 |
| 0 |
0 |
1 |
0 |
0 |
| 0 |
0 |
0 |
1 |
0 |
|
, |
| 0 |
0 |
0 |
0 |
1 |
| 0 |
0 |
0 |
1 |
0 |
| 0 |
0 |
1 |
0 |
0 |
| 0 |
1 |
0 |
0 |
0 |
| 1 |
0 |
0 |
0 |
0 |
|
|
] |
Type: List(Matrix(Integer))
d6 := dihedralGroup(6)
< (1 2 3 4 5 6), (1 6 ) (2 5) (3 4 )>
Type: PermutationGroup(Integer)
toTable()$toFiniteGroup(d6,1)
| i |
a |
b |
aa |
ab |
ba |
aaa |
aab |
baa |
bab |
aaaa |
aaab |
| a |
aa |
ab |
aaa |
aab |
b |
aaaa |
aaab |
ba |
i |
bab |
baa |
| b |
ba |
i |
baa |
bab |
a |
aaab |
aaaa |
aa |
ab |
aab |
aaa |
| aa |
aaa |
aab |
aaaa |
aaab |
ab |
bab |
baa |
b |
a |
i |
ba |
| ab |
b |
a |
ba |
i |
aa |
baa |
bab |
aaa |
aab |
aaab |
aaaa |
| ba |
baa |
bab |
aaab |
aaaa |
i |
aab |
aaa |
a |
b |
ab |
aa |
| aaa |
aaaa |
aaab |
bab |
baa |
aab |
i |
ba |
ab |
aa |
a |
b |
| aab |
ab |
aa |
b |
a |
aaa |
ba |
i |
aaaa |
aaab |
baa |
bab |
| baa |
aaab |
aaaa |
aab |
aaa |
bab |
ab |
aa |
i |
ba |
b |
a |
| bab |
i |
ba |
a |
b |
baa |
aa |
ab |
aaab |
aaaa |
aaa |
aab |
| aaaa |
bab |
baa |
i |
ba |
aaab |
a |
b |
aab |
aaa |
aa |
ab |
| aaab |
aab |
aaa |
ab |
aa |
aaaa |
b |
a |
bab |
baa |
ba |
i |
Type: Table(12)
permutationRepresentation(d6,6)
| [ |
| 0 |
0 |
0 |
0 |
0 |
1 |
| 1 |
0 |
0 |
0 |
0 |
0 |
| 0 |
1 |
0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
0 |
0 |
0 |
| 0 |
0 |
0 |
1 |
0 |
0 |
| 0 |
0 |
0 |
0 |
1 |
0 |
|
, |
| 0 |
0 |
0 |
0 |
0 |
1 |
| 0 |
0 |
0 |
0 |
1 |
0 |
| 0 |
0 |
0 |
1 |
0 |
0 |
| 0 |
0 |
1 |
0 |
0 |
0 |
| 0 |
1 |
0 |
0 |
0 |
0 |
| 1 |
0 |
0 |
0 |
0 |
0 |
|
|
] |
Type: List(Matrix(Integer))
(19) -> |
Discussion
See this thread on FriCAS forum

