Permutation

Here we consider alternative ways to represent a permutation type such as:

• 'preimage-image' coding.
• 'vector' coding.
• Cycle notation.

Since they all have pros and cons we need to consider the coding for both and how to convert between them.

Vectors

PermutationGroup uses vectors as an alternative coding to represent permutations (generators and elements of the group). The elements of these vectors use indexes to represent points. I guess vector terminology makes sense because they transform one set of points into another set of points. However I don't think they are vectors in the sense of being elements of a vector space, that is, operations of vector addition and scalar multipication don't seem to be appropriate.

The use of the Vector domain for this does seem to be streaching the FriCAS type system a bit. For instance elements of subgroup are coded as a vector of a vector (Vector Vector NNI) which would not be valid if the type system were fully checked but presumably gets away with it because vectors are defined over Type.

So for example:

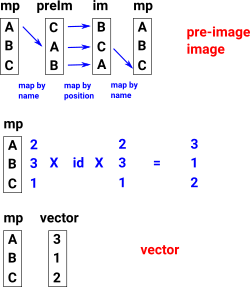
If a permutation is say (1 2 3) the vector is [2,3,1] this means: point 1 maps to point 2 point 2 maps to point 3 point 3 maps to point 1

If a permutation is say (1 2) the vector is [2,1,3] this means: point 1 maps to point 2 point 2 maps to point 1 point 3 maps to point 3

The local function 'perm_to_vec' creates vectors from permutations.

Note on terminology: The word 'index' is overloaded on this page. Here we mean replacing underlying set with NNI values but the word 'index' can also have a different meaning when we define number of cosets like this: [G : H].

Preim-im to vector conversion

We can translate a permutation using 'preimage-image' coding to 'vector' coding like this:

EuclideanSpace

home

Computer Algebra Systems

On this page I have put some information about computer algebra systems and in particular Axiom/FriCAS.

Other Code

This is one of a series of pages describing code that I have written for FriCAS. Some of this code has already been included with the FriCAS library and so can be used as soon as FriCAS is installed (as described here). Other code on these pages is not yet included with FriCAS and so would have to be compiled from within FriCAS. For an overview of all the code I have written, on various topics, see page here.

Other Group Theory

The FriCAS code for coding these groups is discussed on these pages:

• PermutationGroup
• Presentations

For a wider discussuion of the theory see this page:

• Group Theory.