| Here we join up the top and bottom surfaces, but with a half twist. |  |
| So we get a one sided surface with a single external boundary line. |  |
In the program FriCAS (described here) there is a function: moebiusBand which generates a minimal triangulation of a Möbius band.
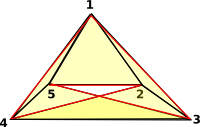
Möbius band: One boundary, shown in red: (2) -> moebiusBand()
+1 2 3+
|2 3 4|
(2) |3 4 5|
|1 4 5|
+1 2 5+
Type: FiniteSimplicialComplex(VertexSetAbstract) |
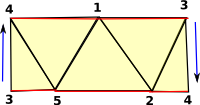
This diagram can only be realised in 3D, to make it clearer in 2D I have duplicated nodes 3 and 4:
The blue arrows should join up, notice the head of the arrow is at the top on the left and bottom on the right. |
Möbius Band - Example of Torsion
If Z represents all the ways a path can wind around a hole then Z/2 might occur in a shape such as a Möbius band where a path has to go round twice to get back to where it started. |
|
 |
Here is a simplicial complex for the Möbius band. The two blue arrows are glued together in the direction shown to give a twist in the band. I've divided the square into 2 triangles to make it into a simplicial complex although that's not very relevant here. |
In this diagram I have taken a second copy of the Möbius band, the second one is flipped vertically, so that they fit together The red arrows indicate a path twice around the band so that it gets back to where it started and forms a cycle. |
 |
 |
As we go around this cyclic path we can go in the direction of the oriented edges (indicated by black arrows) and also in the opposite direction. At each vertex we can add up the edges where an incoming (black) arrow is +1 and an outgoing arrow is -1. So if the path is in the same direction of the edges then the incoming and outgoing edges cancel out and each vertex has the value 0. Where two edges meet at the vertex we get the value +2. Where two edges exit the vertex we get the value -2. So the value of the path at each vertex is always an even number. This is because we are using integers (Z). If we could use fractional values (Field) in the matrix we could arrange for the vertex values along the path to be -1,0 or +1. |
More detail, for instance, mapping Möbius band to circle on page here.
