Maths - Semidirect Product

This is a modification to the direct product described on this page. Here we will apply a mapping to one of the operands before applying the direct product:

{n, h}&22CA;φ {n',h'} = {n * φ(n') , h o h' }

where:

Here we are using the right handed semidirect product &22CA;, we can change to the left handed semidirect product&22C9;by exchanging the operands.

The mapping is done as follows, we first generate cosets of the first group, we apply the group operation to these cosets but slightly modified as follows:

We then use a mapping of the second group to select which coset to use for each product of the second group.

Example C2&22CA;C3

As with the direct product example we will try calculating the product of C2 and C3. As a reminder these are the definitions of these groups individually (full definitions on this page):

C2

generator cayley graph table permutation representation
<m | m²> c2 graph
1 m
m 1
< ( 1 2 ) >
0 1
1 0

C3

generator cayley graph table permutation representation
<r | r³> c3 graph
1 r r²
r r² 1
r² 1 r
< ( 1 2 3 ) >
0 0 1
1 0 0
0 1 0

direct product C3 × C2

This gives :

generator cayley graph table
<m,r | m²,r³,rm=mr> c3c2 graph
{1,1} {r,1} {r²,1} {1,m} {r,m} {r²,m}
{r,1} {r²,1} {1,1} {r,m} {r²,m} {1,m}
{r²,1} {1,1} {r,1} {r²,m} {1,m} {r,m}
{1,m} {r,m} {r²,m} {1,1} {r,1} {r²,1}
{r,m} {r²,m} {1,m} {r,1} {r²,1} {1,1}
{r²,m} {1,m} {r,m} {r²,1} {1,1} {r,1}
permutation representation  
<(1 2 3)(4 5 6),(1 4)(2 5)(3 6)>
[
0 0 1 0 0 0
1 0 0 0 0 0
0 1 0 0 0 0
0 0 0 0 0 1
0 0 0 1 0 0
0 0 0 0 1 0
,
0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1
1 0 0 0 0 0
0 1 0 0 0 0
0 0 1 0 0 0
]

Note that, in addition to applying both the generators and constrains for the original groups we have had to apply an additional constraint: rm=mr. If we had not done this we would have the infinite free product.

Generating a Semidirect Product using a Program

We can use a computer program to generate these groups, here I have used Axiom/FriCAS which is described here. 

(1) -> )r axiom/semidirectProduct
)set output algebra off
)set output mathml on
-- first try C2 x C3
C2 := FiniteGroup(2,[[1,2],[2,1]],["1","m"])
                                                               Type: Type
SDP := semidirectProduct([[1,2,3],[2,3,1],[3,1,2]],["1","r","rr"],
                                    [[2,2,2],[2,2,2],[2,2,2]])$C2

                                                               Type: Type
toTable()$SDP
1 r rr m mr mrr
r rr 1 mr mrr m
rr 1 r mrr m mr
m mr mrr 1 r rr
mr mrr m r rr 1
mrr m mr rr 1 r 
                      
                           

                                                           Type: Table(6)
setGenerators([false,true,false,true,false,false])$SDP
                                                               Type: Void
PSDP := toPermutation()$SDP
<(1 2 3)(4 5 6),(1 4)(2 5)(3 6)> 
                           
                                

                                          Type: PermutationGroup(Integer)
permutationRepresentation(PSDP,6)
[
0 0 1 0 0 0
1 0 0 0 0 0
0 1 0 0 0 0
0 0 0 0 0 1
0 0 0 1 0 0
0 0 0 0 1 0
,
0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1
1 0 0 0 0 0
0 1 0 0 0 0
0 0 1 0 0 0
] 
                      
                           

                                              Type: List(Matrix(Integer))
-- then try C3 x C2 with mapping [[2,2],[2,2]]
C3 := FiniteGroup(3,[[1,2,3],[2,3,1],[3,1,2]],["1","r","rr"])

                                                               Type: Type
SDP := semidirectProduct([[1,2],[2,1]],["1","m"],[[2,2],[2,2]])$C3

                                                               Type: Type
toTable()$SDP
1 m rr rrm r rm
m 1 rrm rr rm r
r rm 1 m rr rrm
rm r m 1 rrm rr
rr rrm r rm 1 m
rrm rr rm r m 1 
                      
                           

                                                           Type: Table(6)
setGenerators([false,true,true,false,false,false])$SDP
                                                               Type: Void
PSDP := toPermutation()$SDP
<(1 2)(3 4)(5 6),(1 3 5)(2 4 6)> 
                           
                                

                                          Type: PermutationGroup(Integer)
permutationRepresentation(PSDP,6)
[
0 1 0 0 0 0
1 0 0 0 0 0
0 0 0 1 0 0
0 0 1 0 0 0
0 0 0 0 0 1
0 0 0 0 1 0
,
0 0 0 0 1 0
0 0 0 0 0 1
1 0 0 0 0 0
0 1 0 0 0 0
0 0 1 0 0 0
0 0 0 1 0 0
] 
                      
                           

                                              Type: List(Matrix(Integer))
-- then try C3 x C2 with mapping [[1,1],[2,2]]
C3b := FiniteGroup(3,[[1,2,3],[2,3,1],[3,1,2]],["1","r","rr"])

                                                               Type: Type
SDP := semidirectProduct([[1,2],[2,1]],["1","m"],[[1,1],[2,2]])$C3b

                                                               Type: Type
toTable()$SDP
1 m r rm rr rrm
m 1 rrm rr rm r
r rm rr rrm 1 m
rm r m 1 rrm rr
rr rrm 1 m r rm
rrm rr rm r m 1 
                      
                           

                                                           Type: Table(6)
setGenerators([false,true,true,false,false,false])$SDP
                                                               Type: Void
PSDP := toPermutation()$SDP
<(1 2)(3 6)(4 5),(1 3 5)(2 4 6)> 
                           
                                

                                          Type: PermutationGroup(Integer)
permutationRepresentation(PSDP,6)
[
0 1 0 0 0 0
1 0 0 0 0 0
0 0 0 0 0 1
0 0 0 0 1 0
0 0 0 1 0 0
0 0 1 0 0 0
,
0 0 0 0 1 0
0 0 0 0 0 1
1 0 0 0 0 0
0 1 0 0 0 0
0 0 1 0 0 0
0 0 0 1 0 0
] 


                                              Type: List(Matrix(Integer))
(19) ->

Examples

Here are some examples of the semidirect product of groups:

Type Product Description
Dihedral
Group 	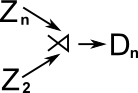	dihedral group as semidirect product The dihedral group is the semidirect product of a cyclic group of order 2 and a cyclic group of order n
Isometries 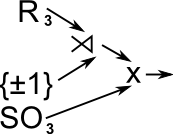isometry as semidirect product

Isometries (distance preseving maps) in 3-space is the semidirect product of:

  • R3 : Addative group of translations.
  • {±1} : Reflections through the origin.
  • SO3 : Group of rotations in 3-space.
Poncaré 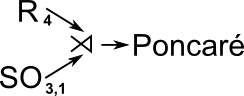poncare group as semidirect product

Poncaré group is the semidirect product of:

  • R4 : Addative group of translations in 4-space.
  • SO3,1 : Lorentz group.

 

metadata block
see also:

 
Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.
flag flag flag flag flag flag The Princeton Companion to Mathematics - This is a big book that attempts to give a wide overview of the whole of mathematics, inevitably there are many things missing, but it gives a good insight into the history, concepts, branches, theorems and wider perspective of mathematics. It is well written and, if you are interested in maths, this is the type of book where you can open a page at random and find something interesting to read. To some extent it can be used as a reference book, although it doesn't have tables of formula for trig functions and so on, but where it is most useful is when you want to read about various topics to find out which topics are interesting and relevant to you.

Terminology and Notation

Specific to this page here:

 

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.