There are some issues with taking the relative angle between two angles, especially if we use this formula:
atan2(v2.y,v2.x) - atan2(v1.y,v1.x)
as discussed on this page.
It is useful to keep in mind that:
- We can always add or subtract 360° (or in radians 2π) to any angle without changing the angle it represents (because after 360° we get back to where we started ). In most implementations atan2 will return a value between +π and -π but if we want a value between 0 and 2π then we could add 2π to negative values.
- If atan2 returns a value between +π and -π then
atan2(v2.y,v2.x) - atan2(v1.y,v1.x)
could return a value between +2π and -2π so if it is above +π we might want to subtract 2π and if it is below -π we might want to add 2π. - If we are facing in direction 1 and we want to rotate to face in direction 2 we could rotate clockwise or anti-clockwise. So a rotation of pi/2 in the clockwise direction is the same as in the anti-clockwise direction 3pi/4. So we need to be clear if we always want to rotate in a clockwise direction or if we want to rotate clockwise or anti-clockwise depending on which is the smaller angle.
So, as an example, lets look at two vectors which are 90° (π/2) apart relative to each other. It should not matter what coordinate system we use as follows:
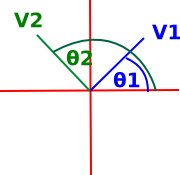 |
If v1 is in the first quadrant and v2 is in the second we might get: atan2(-1,1) - atan2(1,1) = 3/4π - 1/4π = π/2 |
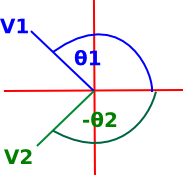 |
If v1 is in the second quadrant and v2 is in the third we might get: atan2(-1,-1) - atan2(-1,1) = -3/4π - 3/4π = -π3/2 adding 2π gives: = π/2 |
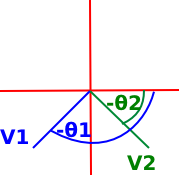 |
If v1 is in the third quadrant and v2 is in the forth we might get: atan2(1,-1) - atan2(-1,-1) = -1/4π + 3/4π = π/2 |
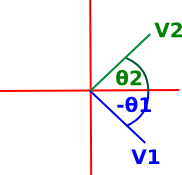 |
If v1 is in the forth quadrant and v2 is in the first we might get: atan2(1,1) - atan2(1,-1) = 1/4π + 1/4π = π/2 |
So the angle between the vectors is always π/2.
