Given a quaternion representing a 3D rotation through an angle theta, how do we find the quaternion which represents a rotation, in the same direction, but through half that angle.

Thank you to minorlogic who has sent me the answer here.

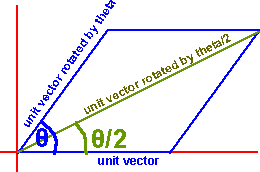
The above diagram shows the situation using vectors. We have a unit vector rotated by theta, and a non-rotated unit vector. To get a vector rotated by theta/2 we just have to add the two vectors together as shown above.

The strange thing is that we can do the same using quaternions to represent the rotation. For example if we have a quaternion representing a rotation by theta:

q(x,y,z,w).

Then we can add a unit quaternion q(0,0,0,1) and normalise to get a quaternion representing the mid angle of the rotation.

qHalf = norm(q(x,y,z,w+1))

This seemed strange to me because usually we combine quaternions by multiplying them. So if we have a quaternion q1 representing a rotation by angle1 and we have a quaternion q2 representing a rotation by angle2, if we want to rotate by angle1 followed by angle2, this would be represented by q1*q2. Usually the addition operation is not meaningful when quaternions are used to represent rotations.

I think the reason that addition works in this special case is that all rotations are about the same axis.

For more information see message from minorlogic.

This is also related to the page about calculating the angle between two vectors.