As we have already seen here, rotations in 3 dimensions have 3 degrees of freedom but if we work purely in 3 dimensions they are non-linear, have singularitys, are difficult to combine and are generally messy to work with.
The solution is to map our 3D rotational space to a subset of 4 dimensional space. We don't just extrude our world into a fourth dimension, instead we map it onto the hyper-surface of a 4 dimensional sphere.
So to do some operation with rotations, such as combining two subsequent rotations, we need to follow the following sequence:
- Take our rotations in the 3D world and translate them onto the 4D domain (that is: convert them to quaternions).
- Do the corresponding operation in the 4D domain (in this case multiply the two quaternions).
- Translate the result back to our 3D world.

If we have a quaternion a + i b + j c + k d to be used to represent rotations then we normalise so that:
a2 + b2 + c2 + d2=1
Which is what we would get if a, b, c and d were coordinates of points on a 4D sphere
It wouldn't work if we squared the part including the imaginary operators: a2 + (i b)2 + (j c)2 + (k d)2
Which would give:
a2 - b2 - c2 - d2
Rotation and Scaling
Imagine that the four dimensions of the quaternion are all drawn perpendicular to each other, this is a bit difficult to draw in 2 dimensions, so we will crunch the 3 imaginary dimensions together for ease of drawing:
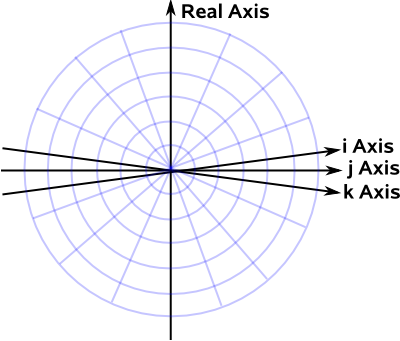
On this diagram a straight line through the origin contains all the 4D points representing the same rotation. The red line below might represent, for example, 90° about the y axis.
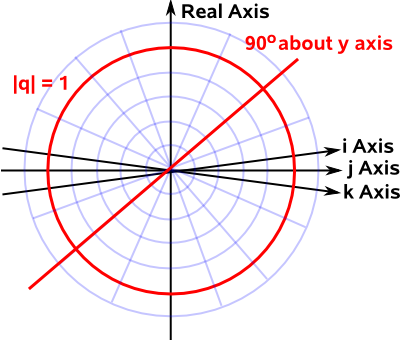
As we move along the line we get different scaling factors.
If q = w + x i + y j + z k
where:
- q = a quaternion
- w,x,y,z = normalised coordinates of the quaternion
then α q = α w + α x i + α y j + α z k
where:
- α = a scalar scaling factor, the actual scaling factor is α²
This scaling factor does not effect the rotation, only the magnitude of the output.
If α = 1, that is no scaling just pure rotation, that will be represented by the red circle on the diagram above.
We can see from the diagram that there are two places, representing two quaternions, that the red line and the red circle intersect. So there are two quaternions that represent every rotation, we know that from other pages, but its nice to have it confirmed graphically.