First we will calculate the simple case of a square then we go on to use binomial theorem to calculate the more general case of zn
where:
- n is an integer.
- z is a double number.
Square
| z plane | w plane | |
|---|---|---|
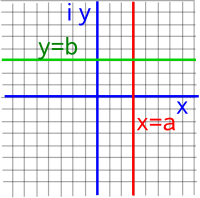 |
--> w=z² |
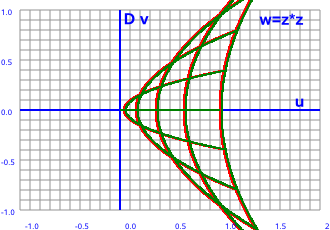 |
Pure real values always square to a positive value and pure imaginary values always square to a negative value. However real and imaginary parts together cover the whole plane.
Let the components of the input and output planes be:
z = x + D y and w = u + D v
lets take the example of the square function w = z²
so:
w = (x + D y)²
multiplying out gives:
w = x² + y² + D 2 x y
so the u and v components are:
u = x² + y²
v = 2 x y
Using Binomial Theorem
We want to calculate an expression for:
(z)n
where:
- n is an integer.
- z is a double number.
We can use the binomial theorem:
| (a + D b)n= |
|
|
(-D)k a n-k bk |


