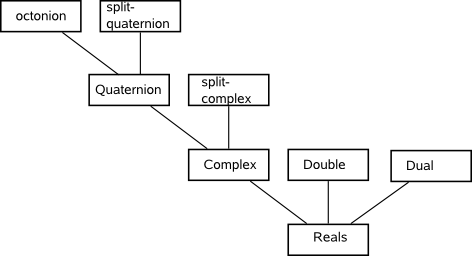
This builds, complex-numbers,quaternions, octonions, sedenions...
The multipication table for complex numbers is:
| (a+ i b)*(c+ i d) | dimension=1 |
dimension=i value=d |
| dimension=1 value=a |
dimension=1 value=ac |
dimension=i value=ad |
| dimension=i value=b |
dimension=i value=cb |
dimension=1 value=-db |
However, if a,b,c and d are not real numbers but are higher order elements, such as complex numbers, we need to modify the table slightly (the modification has no effect on real numbers):
| (a,b)(c,d) | dimension=1 |
dimension=i value=d |
| dimension=1 value=a |
dimension=1 value=ac |
dimension=i value=a'd |
| dimension=i value=b |
dimension=i value=cb |
dimension=1 value=-db' |
where:
- x' is the conjugate of x so we have (a,b)' = (a, -b)
Alternativley the Cayley-Dickson construction is often expressed in these terms:
(a,b)(c,d) = (ac - db' , a'd + cb)
which gives the individual terms:
ac = (ac,0)
ad = (0,a'd)
bc = (0,cb)
bd = (-db',0)
Example
Say we want to combine two complex numbers to give quaternion algebra:
In that case a,b,c and d are complex numbers, lets call them:
ax + i ay, bx + i by, cx + i cy and dx + i dy
so we get:
(ax + i ay,bx + i by)(cx + i cy,dx + i dy)
multiplying out these terms (see this page for full working) gives 4 real numbers:
- ax cx- ay cy - dx bx - dy by
- ay cx + ay cx + dx by - dy bx
- ax dx + ay dy + cx bx - cy by
- cy bx + cx by - ay dx- ax dy
which is the same as quaternion multipication from this page:
z1 * z2= a*e - b*f - c*g- d*h + i (b*e + a*f + c*h - d*g) + j (a*g - b*h + c*e + d*f) + k (a*h + b*g - c*f + d*e)
Construct from Kronecker product
We can build up a very similar hierarchy of algebras using complex, double and dual numbers as follows:
| designation | multiplication table | type | ||||
|---|---|---|---|---|---|---|
| C |
|
complex | ||||
| Do |
|
double | ||||
| Du |
|
dual |
Like the Clifford algebras these are characterised by what they square to, 'C' squares to -1, 'Do' squares to +1 and 'Du' squares to 0 so we can build up more and more complex algebras by combining these in different ways using the Kronecker product, this will allow us to generate all of the Clifford algebras.
For example we could generate C![]() C as follows: first we take C given by:
C as follows: first we take C given by:
| a*b | a=real | b=i |
| a=real | 1 | i |
| b=i | i | -1 |
We want to combine this with another copy of 'C', this requires another independent dimension so this time we will use j instead if i:
| c*d | c=real | d=i |
| c=real | 1 | j |
| d=i | j | -1 |
| (a + i b)(c + j d) | c | d |
| a | ac | a'd |
| b | cb | -db' |
| a |
|
|||||||||||
| a*d= |
|
= |
|
j | ||||||||
| cb= |
|
= |
|
j | ||||||||
| -db*= |
|
= |
|
|
|||||||||||||
|
|
| We can define the conjugate |
|
* |
to give |
|
so we get:
|
|
||||||||||||
|
|
When we multipy out the terms we get:
| 1 | i | j | i^j |
| i | -1 | i^j | -j |
| j | -i^j | -1 | i |
| i^j | j | -i | -1 |
which is the table for quaternion
Cayley-Dickson
quaternion (complex containing complex) |
complex containing double | double containing complex | double containing double | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i & j anticommute i*j = -j*i |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| i & j commute i*j = j*i |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
i & j anticommute but lefthanded |
|
|
|
|
how these results were generated.
As the above link explains, the table was generated by a computer program from the (modified) Caley-Dickson doubling process.
Alternative Method
We combine these using the Kronecker product, by taking all combinations of i and j, that is: 1, i, j, i^j. Then put in 4×4 array going across the table (red) and down (blue) which gives:
| 1^1 | 1^i | 1^j | 1^i^j |
| i^1 | i^i | i^j | i^i^j |
| j^1 | j^i | j^j | j^i^j |
| i^j^1 | i^j^i | i^j^j | i^j^i^j |
We can simplify this by using the individual tables to give us the following identities:
- 1^x=x
- x^1=x
- j^i = - i^j
- i^i = -1
- j^j = -1
Which gives:
| 1 | i | j | i^j |
| i | -1 | i^j | -j |
| j | -i^j | -1 | i |
| i^j | j | -i | -1 |
This is exactly the same as G 0,2,0 which is a geometric algebra based on two dimensions which both square to -ve, shown here:
| e | e1 | e2 | e12 |
| e1 | -e | e12 | -e2 |
| e2 | -e12 | -e | e1 |
| e12 | e2 | -e1 | -e |
This table was generated using the program described on this page
Its not surprising the table is the same (with only notation differences) as is was derived in the same way.
But here is where the division algebras diverge from geometric algebra, in geometric algebra terms like i^i are called bivectors and remain in that form as they can't be simplified any further, in division algebras like this we convert the bivector terms into vectors like this:
let k=i^i
This gives,
| 1 | i | j | k |
| i | -1 | k | -j |
| j | -k | -1 | i |
| k | j | -i | -1 |
If we only did this at the end of the calculation it would not matter since we have already shown that:
C![]() C = H = G 0,2,0
C = H = G 0,2,0
But we are going on to build up further algebras from this and since the vector base k has slightly different properties to the bivector base i^i then the algebras are going to diverge more and more as we build up more complex algebras.
For instance, if we add another multiplication by C to give octonions,
C![]() C
C![]() C = O
C = O
This can cause non-associativity because the![]() operator involves converting bivector bases to vector bases and vector×bivector may involve a sign change from bivector×vector. So it may be that:
operator involves converting bivector bases to vector bases and vector×bivector may involve a sign change from bivector×vector. So it may be that:
(C![]() C)
C)![]() C ≠ C
C ≠ C![]() (C
(C![]() C) ?
C) ?
This may become even more ambiguous for 16ions, do we define them as (C![]() C)
C)![]() (C
(C![]() C) or C
C) or C![]() (C
(C![]() C)
C)![]() C ?
C ?
We can calculate the result as follows:
The terms of C![]() C are 1,i,j,k and we will multiply this by a third complex number, say,
C are 1,i,j,k and we will multiply this by a third complex number, say,
| 1 | m |
| m | -1 |
which gives the product:
| 1^1 | 1^i | 1^j | 1^k | 1^m | 1^i^m | 1^j^m | 1^k^m |
| i^1 | i^i | i^j | i^k | i^m | i^i^m | i^j^m | i^k^m |
| j^1 | j^i | j^j | j^k | j^m | j^i^m | j^j^m | j^k^m |
| k^1 | k^i | k^j | k^k | k^m | k^i^m | k^j^m | k^k^m |
| m^1 | m^i | m^j | m^k | m^m | m^i^m | m^j^m | m^k^m |
| i^m^1 | i^m^i | i^m^j | i^m^k | i^m^m | i^m^i^m | i^m^j^m | i^m^k^m |
| j^m^1 | j^m^i | j^m^j | j^m^k | j^m^m | j^m^i^m | j^m^j^m | j^m^k^m |
| k^m^1 | k^m^i | k^m^j | k^m^k | k^m^m | k^m^i^m | k^m^j^m | k^m^k^m |
simplifying gives:
| 1 | i | j | k | m | i^m | j^m | k^m |
| i | -1 | k | -j | i^m | -m | k^m | -j^m |
| j | -k | -1 | i | j^m | -k^m | -m | i^m |
| k | j | -i | -1 | k^m | j^m | -i^m | -m |
| m | -i^m | -j^m | -k^m | -1 | i | j | k |
| i^m | m | -k^m | j^m | -i | -1 | k | -j |
| j^m | k^m | m | -i^m | -j | -k | -1 | i |
| k^m | -j^m | i^m | m | -k | j | -i | -1 |
again we convert bivectors to vectors as follows:
i =e1, j=e2, k=e3, m=e4, i^m=e5, j^m=e6, k^m=e7
which gives:
| 1 | e1 | e2 | e3 | e4 | e5 | e6 | e7 |
| e1 | -1 | -e3 | e2 | -e5 | e4 | e7 | -e6 |
| e2 | e3 | -1 | -e1 | -e6 | -e7 | e4 | e5 |
| e3 | -e2 | e1 | -1 | -e7 | e6 | -e5 | e4 |
| e4 | e5 | e6 | e7 | -1 | -e1 | -e2 | -e3 |
| e5 | -e4 | e7 | -e6 | e1 | -1 | e3 | -e2 |
| e6 | -e7 | -e4 | e5 | e2 | -e3 | -1 | e1 |
| e7 | e6 | -e5 | -e4 | e3 | e2 | -e1 | -1 |
which is the multiplication table for octonions.
I have not yet worked out the table when the terms are combined in a different order, my plan is to adapt the program here to do this. Such a program would become more necessary as we build really big algebras (for example E8).

