There are many starting points (postulates) for deriving the consequences of Special Relativity. For instance:
- From the independence of the laws of physics to the linear movement of the frame of reference combined with the speed of light being the same in all these frames.
- From the Minkowski metric, that is the formula for 'distance' or 'interval' in 4 dimensional space-time.
- From the curvature of space-time, that is 4 dimensional hyperbolic space.
These all define the curvature of space-time and from any of these sets of postulates we can derive the Lorentz Transform. The Lorentz Transform shows how space and time alter for observers traveling at different velocities. Its a transform of space-time between frames of reference traveling at different velocities.
From this point we can investigate the dynamics of space-time such as the laws of energy-momentum which might be derived using Noethers theorem and so to the results concerning the equivalence of energy and matter.
Constant Speed of light
As discussed here relativity applies to Newtonian physics, but there is a problem, light.
Light does not have mass, it is an electromagnetic wave. A change in an electric field causes a magnetic field and a change in an magnetic field causes a electric field this will continue as a photon. These fields were described by Faraday and Maxwell worked out the mathematics of this. The speed of the photon is determined by the electromagnetic properties of the material that it travels through.
So what about when the photon is traveling through a vacuum? In this case what will its velocity be relative to?
Do we need the concept of an either which the velocity of a photon will move relative to?
Can we use a photon to determine the absolute velocity of our frame-of-reference (thereby breaking the relativity principle)?
Einstein proposed that the velocity of a photon in a vacuum will be a constant known as 'c'. This velocity will be the same regardless of the velocity of the frame of reference of the observer. So several observers, all moving relative to each other, will nevertheless all see the photon traveling at the same speed.
Postulates:
- The laws of physics are the same for all observers independent of how any given observer may be moving through space, in other words, there is no experiment one can do that will distinguish one observers frame-of-reference as somehow 'preferred' (closer to being at rest with respect to the universe as a whole) over that of any other observer. (this applies to both Newtonian and Einstianian physics.
- The speed of light, through a vacuum, will always be the same regardless of the frame-of-reference of the observer.
Effect of velocity on time
We can construct a clock with two mirrors a fixed distance apart (say 1m) and then set a photon reflecting back and forward between the mirrors.

If we put this clock on a moving train we can measure the effect of velocity on time.
First measure time in the frame of reference of the train. If the mirrors are 1m apart then, the time taken for the photon to travel from one mirror to the other is:
t0= 1/c
where
- t0= time in frame of reference of train
- c = speed of light
The horizontal distance traveled by the train will be:
x = v tv = v/c
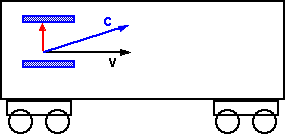
We now measure the time from the frame-of-reference of the ground. From this reference the photon appears to travel at an angle which is the sum of its vertical and horizontal components. This velocity of the photon will be c.
So the time in the frame of reference of the ground will be:
tv= distance / c
The distance is the vector sum of 1m in the vertical direction and v t0 in the horizontal direction (this horizontal distance traveled by the train will be the same as the above case because its perpendicular to the direction of the light).
So,
distance2 = 1 + (v/c)2
Therefore,
tv= distance / c = √(1 + (v/c)2) /c
tv= t0 √(1 + (v/c)2)
or
t0= tv / √(1 + (v/c)2)
since this factor occurs frequently in special relativity we often represent it by ![]() (gamma) so,
(gamma) so,
t0= tv ![]()
where:
- tv= time interval in the moving frame of reference relative to the observer.
- t0= time interval in the frame of reference of the observer.
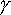 = 1 / √(1 + (v/c)2)
= 1 / √(1 + (v/c)2)
Therefore when the clock is moving relative to the observer the time interval is longer and therefore it appears to be running slow.
Effect of velocity on distance
This time we turn the mirrors round so that the light is traveling in the same direction as the train.

Again, in the frame of reference of the train, and assume mirrors are 1m apart then, the time taken for the photon to travel from one mirror to the other is:
tv= 1/c
where
- tv= time in frame of reference of train
- c = speed of light
The horizontal distance traveled by the train will be:
xv = v tv = v/c
Now we repeat in the frame of reference of the ground, the horizontal distance traveled by the train will be:
x0 = v t0
x0= v tv √(1 + (v/c)2)
x0= xv √(1 + (v/c)2)
so
xv= x0 ![]()
So the apparent distance of a moving object appears to be shortened in the direction of the velocity, however distance perpendicular to the velocity does not change, we can prove this by using symmetry.

Imagine two rings A and B, approaching each other at high speed, if size did change perpendicular to the velocity then:
- In the frame of reference of A then B will reduce in size, therefore B will pass inside A.
- In the frame of reference of B then A will reduce in size, therefore A will pass inside B.
A cant be simultaneously inside and outside of B, so this type of perpendicular size reduction cant happen.
We can combine the time dilation, and distance change in the direction of the velocity but not perpendicular, can be combined to give the Lorentz transform here.
Invariant interval
Two events that are simultaneous for one observer are not generally simultaneous for another. If two events e1 and e2 are separated by length L and time T. These values will depend on the reference frame of the observer.
The invariant interval ![]() is:
is:
![]() 2= T 2- (L/c) 2
2= T 2- (L/c) 2
This is the separation between the two events in space-time. The invariant interval between any two events must be the same for all observers, no matter how they are moving relative to each other.
L' = ![]() (L - v T)
(L - v T)
T' = ![]() (T - v L/c2)
(T - v L/c2)
For special relativity the symmetry of the invariant interval replaces the symmetry of time for Galilean physics.
Mass-Energy
According to Noethers theorem every Symmetry has a corresponding physical constant.
| Symmetry | Physical constant |
The invariant interval
|
Energy-Momentum m2c4=E2 - p2c2 |
where:
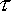 = invariant interval
= invariant interval- T = time
- L = length
- c = speed of light
- m = rest mass
- E = energy
- p = momentum
When the mass is stationary p=0 and the equation becomes;
Energy of stationary mass = m c2
If v is low compared to c the equation becomes:
E = m c2 + p2 /2m + ...
Which is roughly:
E = m c2 + 1/2 m v2
Energy = rest mass + kinetic energy
Kinetic Energy
The Kinetic Energy in the frame of reference of the mass = 0.5 m v2
Mass = gravitational charge
Potential Energy
Potential Energy is a form of energy that's stored in an object by virtue of the object being under the influence of some force.
