On these pages we look at some interesting concepts, we look at curved space: what curved space means, how we can tell if a space is curved from inside it or from outside it.
We look at how we can embed on type of space inside another and see that we can map between different spaces in different ways.
We also look at compacification and how we can represent infinitely large and infinitesimally small vectors in our spaces in ways that do not do not lead to singularities and other problems.
These concepts turn out to be useful, even when we are working with flat space, we will find ways to represent vectors and planes that do not go through the origin. This gives us ways to represent rotations and translations as a single operation.
The other application is relativistic space-time.
Rienmannian Geometry
In Rienmannian geometry space can curve at different places (see manifolds) here we look at geometries where the curve of space is constant.
|
flat space |
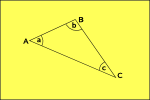 |
|
space curves outward |
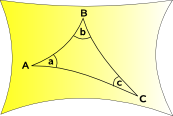 |
Spherical Geometry and Elliptic Geometry space curves inward |
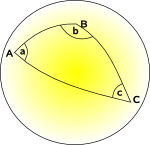 |
In a curved (Non-Euclidean) geometry we cannot find a set of coordinates which are mutually perpendicular, where the coordinate lines are all parallel to each other and where each grid square has the same area. We may possibly find a coordinate system where we can do some of these but not all.
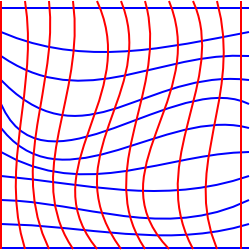
This diagram tries to illustrate this situation in 2 dimensions, although its a bit misleading, because we have drawn it on a plane so we could have drawn rectangular coordinates.
To try to illustrate a situation where this is impossible we could think of a two dimensional plane which has been stretched into the third dimension.

In this situation we can choose coordinates which form a rectangular grid when projected onto a horizontal plane, however, to a person living in the surface then some of the grid squares will appear to have a larger area than others and the grid lines may not appear to be parallel. There is no two dimensional coordinate system that will preserve parallel lines, angles and areas at the same time.
A similar example is trying to map the surface of the earth, we can use latitude and longitude lines but the longitude lines get closer nearer the poles.
In these cases we could work in terms of 3 dimensional coordinates and that is an approach we will take with some types of non-Euclidean geometries. It is often possible to embed a particular geometry in a higher dimensional geometry in order to make it more Euclidean.
It is sometimes the case that, when we look at a geometry on a large scale that it is non-Euclidean, but if we look at it on a smaller and smaller scale then it approximates to a Euclidean geometry. To do this we need to find a coordinate system where angles are preserved at every point, that is, the horizontal and vertical coordinate lines need to always intersect at 90° even though the lines may not be straight. This is known as a conformal geometry. In this type of geometry we can at least define a local coordinate system.
Related to this is whether the geometry can be differentiated and integrated, a condition for this is that it must be well behaved and not have any sudden jumps etc. Some geometries and coordinate systems may be well behaved in some places but have singularities etc.
For discussion about how curvature is measured see this page.
Mathematical Notation
How do we deal with geometries where we can't use all the rules that apply to euclidean geometry?
One approach is to use tensor notation, this provides conventions and notation which help us in switching between different coordinate systems. An orthogonal coordinate system, local to any point, can be defined by using basis vectors which are tangents to the coordinate lines.
Manifold
see this page
Relationship between Hyperbolic and Minkowski Geometries
| Minkowski Geometry | Hyperbolic Geometry | |
| point | event in space time | particle in uniform motion |
| distance between two points | space-time interval between two events | relative speed between two such particles |
Terminology
Here we look at the terminology such as geometries, spaces, models, projections and transforms. Its quite difficult when we start dealing with non-Euclidean geometries because we use similar terminology that we are used to in conventional Euclidean space but the terms can have slightly different properties. For example, the concept of a 'line' can look different in different geometries:

Geometries and Spaces
Rienmannian geometry defines spaces generally in terms of manifolds, here we are interested in homogeneous, isotropic spaces which have no preferred points or directions, examples are:
| parallel postulate - number of unique parallel lines through point | space curves | Inventors | Point at Infinity | Distance Measure | |
|---|---|---|---|---|---|
| Eulidean Geometry | 1 | none | Euclid | where parallel lines meet | √(x² + y²) |
| Hyperbolic Geometry | ∞ | space curves outward so lines dont meet | Lobachevskii and Bolyai |
||
|
Elliptic Geometry |
0 | space curves inward so all lines meet |
Models
Examples are:
- Upper half-plane model
- Poincare disc model
- Projective model
- Conformal model
Projections
Transforms
Invariant
Examples are:
- Möbius Transform
- Lorentz Transform
Parallel Postulate
If we take away the parallel postulate from Euclidean Space.
This leads to:
- parallel postulate is false
- the angles of a triangle do not add to π
- for a shape of a given size, there does not in general, exist a similar shape of a larger size.
Possible mappings between Euclidean Space and Hyperbolic Space:
properties:
| projective | conformal (Poincaré disc ) | |
|---|---|---|
| straight lines - geodesics | segments of circles | |
| angle | preserved | |
| internal angles of triangle | π-(α+β+γ)=CΔ | |
| distance between two points | ln | |
Next
There are many types of non-Euclidean geometry:

