Cylindrical coordinates allow points to be specified using two linear distances
and one angle. These three coordinates are shown on the diagram as:
- r = radius (distance from axis of cylinder)
- h = height (distance along axis of cylinder)
- θ = (sometimes a) = angle around axis.
|
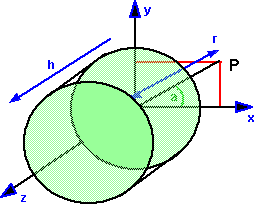 |
Cylinder aligned with the z axis
Cylindrical coordinates to Cartesian coordinates
Cartesian coordinates to Cylindrical coordinates
|
|
= |
| atan2(Cx,Cy) |
| √(Cx2 + Cy2) |
| Cz |
|
Cylinder aligned with the arbitrary axis
Cylindrical coordinates to Cartesian coordinates
We want to rotate the above so that the h axis is aligned with the arbitrary
axis (Ax, Ay, Az) in other words we want to lookat the point (Ax, Ay, Az) see
lookat
|
|
= |
| √(Az2 + Ay2) |
0 |
Ax |
| 0 |
√(Az2 + Ax2) |
Ay |
| -Ax |
-Ay |
Az |
|
|
Multiplying gives:
|
|
= |
| √(Az2 + Ay2) *
r sin(θ)
+ h*Ax |
| √(Az2 + Ax2) * r cos(θ)
+ h*Ay |
| -Ax * r sin(θ)-Ay
* r cos(θ)
+ h*Az |
|
Cartesian coordinates to Cylindrical coordinates
In order to do this we need to invert the above matrix, since this is orthogonal
we can invert by transposing as follows:
|
|
= |
| √(Az2 + Ay2) |
0 |
-Ax |
| 0 |
√(Az2 + Ax2) |
-Ay |
| Ax |
Ay |
Az |
|
|
Multiplying gives,
|
|
= |
| Cx * √(Az2 + Ay2)
- Ax * Cz |
| Cy * √(Az2 + Ax2) -Ay * Cz |
| Cx * Ax + Cy * Ay +Cz * Az |
|
So in terms of θ,
r , h
|
= |
| atan2(Cx * √(Az2 + Ay2)
- Ax * Cz,Cy * √(Az2 + Ax2) -Ay * Cz) |
| √((Cx * √(Az2 + Ay2) - Ax
* Cz)2 + (Cy * √(Az2 + Ax2) -Ay
* Cz)2) |
| Cx * Ax + Cy * Ay +Cz * Az |
|
Using Tensors
This is more advanced stuff and only really needed if you need to do physics or advanced geometry in curvilinear coordinates.
On the curvilinear coordinates page we saw that the expression of coordinates as a linear equation:
ei Ai = e1 A1 + e2 A2 + e3 A3
can be modified for curvilinear coordinates where either the basis or the components depend on the location:
e(x,y,z)i Ai = e(x,y,z)1 A1 + e(x,y,z)2 A2 + e(x,y,z)3 A3…
or
ei A(x,y,z)i = e1 A(x,y,z)1 + e2 A(x,y,z)2 + e3 A(x,y,z)3…
where:
- e(x,y,z) is a basis which is a function of position.
- A(x,y,z) are terms which are functions of position.
We have already looked at the situation where the terms are expressed as a function of a global linear coordinate system. Now lets look at the situation where the linear basis is a function of position. There are two ways to do this:
- they can be built along the coordinate axes (axis-colinear) then the basis vectors
transform like covariant vectors.
- they can be built to be perpendicular (normal) to the
coordinate surfaces then the basis vectors transform like contravariant vectors.
Covariant Axis
| e1 A1 + e2 A2 + e3 A3 = |
∂x |
e1 |
∂θ |
A1 + |
∂y |
e2 |
∂r |
A2 + |
∂z |
e3 |
∂h |
A3 |
| ∂θ |
∂x |
∂r |
∂y |
∂h |
∂z |
where:
| ∂θ |
= |
∂atan2(x,y) |
= |
y |
= |
y |
| ∂x |
∂x |
1 +(x/y)2 |
x2+ y 2 |
| ∂r |
= |
√((x)2) + (y)2) |
|
= 1 |
|
|
| ∂y |
∂y |
|
| ∂h |
|
= 1 |
|
|
|
|
| ∂z |
|
where:
| ∂ |
= cosθ |
∂ |
-r-1sinθ |
∂ |
|
|
| ∂x |
∂r |
∂θ |
|
|
| ∂ |
= sinθ |
∂ |
+r-1cosθ |
∂ |
|
|
| ∂y |
∂r |
∂θ |
|
|
| ∂ |
= |
∂ |
|
|
|
|
| ∂z |
∂h |
|
|
|
|
Jacobean
| J = |
|
= |
|
= |
| cosθ |
sinθ |
0 |
| -r-1sinθ |
r-1cosθ |
0 |
| 0 |
0 |
1 |
|
Inverse Jacobean
| J-1 = |
|
= |
|
= |
| cosθ |
sinθ |
0 |
| r sinθ |
r cosθ |
0 |
| 0 |
0 |
1 |
|
Contravariant Axis
| e1 A1 + e2 A2 + e3 A3 = |
∂θ |
e1 |
∂x1 |
A1 + |
∂r |
e2 |
∂x2 |
A2 + |
∂h |
e3 |
∂x3 |
A3 |
| ∂x1 |
∂θ |
∂x2 |
∂r |
∂x3 |
∂h |


