logo back up home forward   further reading more topics »

Maths - Euler to Quaternion - Sample Orientations

Sample Rotations

In order to try to explain things I thought it might help to work out a simple case where rotations are only allowed in mutiples of 90 degrees. This should make it easier to illustrate the orientation with a simple aeroplane figure, we can rotate this either about the x,y or z axis as shown here:

When we combine these rotations about the x,y and z axies in 90 degree multiples there are 24 possible orientations as shown here:

heading applied first giving 4 possible orientations:

rightUp

reference orientation

heading = 0
attitude = 0
bank = 0

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =1
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =1
s1 = sin(heading/2) =0
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =0

which gives:

w = 1
x = 0
y = 0
z = 0

backUp

rotate by 90 degrees about y axis

heading = 90 degrees
attitude = 0
bank = 0

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =1
s1 = sin(heading/2) =0.7071
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =0

which gives:

w = 0.7071
x = 0
y = 0.7071
z = 0

leftUp

rotate by 180 degrees about y axis

heading = 180 degrees
attitude = 0
bank = 0

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =1
s1 = sin(heading/2) =1
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =0

which gives:

w = 0
x = 0
y = 1
z = 0

forwardUp

rotate by 270 degrees about y axis

heading = -90 degrees
attitude = 0
bank = 0

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =1
s1 = sin(heading/2) =-0.7071
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =0

which gives:

w = 0.7071
x = 0
y = -0.7071
z = 0

Then apply attitude +90 degrees for each of the above: (note: that if we went on to apply bank to these it would just rotate between these values, the straight up and streight down orientations are known as singularities because they can be fully defined without using the bank value) post multiply above by 0.7071 + k 0.7071 to give:

upLeft

heading = 0
attitude = 90 degrees
bank = 0

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =1
c2 = cos(attitude/2) =0.7071
c3 = cos(bank/2) =1
s1 = sin(heading/2) =0
s2 = sin(attitude/2) =0.7071
s3 = sin(bank/2) =0

which gives:

w = 0.7071
x = 0
y = 0
z = 0.7071

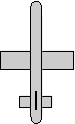
upForward

heading = 90 degrees
attitude = 90 degrees
bank = 0

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =0.7071
c3 = cos(bank/2) =1
s1 = sin(heading/2) =0.7071
s2 = sin(attitude/2) =0.7071
s3 = sin(bank/2) =0

which gives:

w = 0.5
x = 0.5
y = 0.5
z = 0.5

upRight

heading = 180 degrees
attitude = 90 degrees
bank = 0

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0
c2 = cos(attitude/2) =0.7071
c3 = cos(bank/2) =1
s1 = sin(heading/2) =1
s2 = sin(attitude/2) =0.7071
s3 = sin(bank/2) =0

which gives:

w = 0
x = 0.7071
y = 0.7071
z = 0

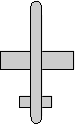
upBack

heading = -90 degrees
attitude = 90 degrees
bank = 0

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =0.7071
c3 = cos(bank/2) =1
s1 = sin(heading/2) =-0.7071
s2 = sin(attitude/2) =0.7071
s3 = sin(bank/2) =0

which gives:

w = 0.5
x = -0.5
y = -0.5
z = 0.5

Or instead apply attitude -90 degrees (also a singularity): post multiply top row by 0.7071 - k 0.7071 to give:

downRight

heading = 0
attitude = -90 degrees
bank = 0

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =1
c2 = cos(attitude/2) =0.7071
c3 = cos(bank/2) =1
s1 = sin(heading/2) =0
s2 = sin(attitude/2) =-0.7071
s3 = sin(bank/2) =0

which gives:

w = 0.7071
x = 0
y = 0
z = -0.7071

downBack

heading = 90 degrees
attitude = -90 degrees
bank = 0

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =0.7071
c3 = cos(bank/2) =1
s1 = sin(heading/2) =0.7071
s2 = sin(attitude/2) =-0.7071
s3 = sin(bank/2) =0

which gives:

w = 0.5
x = -0.5
y = 0.5
z = -0.5

downLeft

heading = 180 degrees
attitude = -90 degrees
bank = 0

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0
c2 = cos(attitude/2) =0.7071
c3 = cos(bank/2) =1
s1 = sin(heading/2) =1
s2 = sin(attitude/2) =-0.7071
s3 = sin(bank/2) =0

which gives:

w = 0
x = -0.7071
y = 0.7071
z = 0

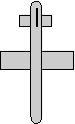
downForward

heading = -90 degrees
attitude = -90 degrees
bank = 0

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =0.7071
c3 = cos(bank/2) =1
s1 = sin(heading/2) =-0.7071
s2 = sin(attitude/2) =-0.7071
s3 = sin(bank/2) =0

which gives:

w = 0.5
x = 0.5
y = -0.5
z = -0.5

Normally we dont go beond attitude + or - 90 degrees because thes are singularities, instead apply bank +90 degrees: post multiply top row by 0.7071 + i 0.7071 to give:

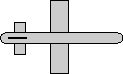
rightForward

heading = 0
attitude = 0
bank = 90 degrees

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =1
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0.7071
s1 = sin(heading/2) =0
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =0.7071

which gives:

w = 0.7071
x = 0.7071
y = 0
z = 0

backRight

heading = 90 degrees
attitude = 0
bank = 90 degrees

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0.7071
s1 = sin(heading/2) =0.7071
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =0.7071

which gives:

w = 0.5
x = 0.5
y = 0.5
z = -0.5

leftBack

heading = 180 degrees
attitude = 0
bank = 90 degrees

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0.7071
s1 = sin(heading/2) =1
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =0.7071

which gives:

w = 0
x = 0
y = 0.7071
z = -0.7071

forwardLeft

heading = -90 degrees
attitude = 0
bank = 90 degrees

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0.7071
s1 = sin(heading/2) =-0.7071
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =0.7071

which gives:

w = 0.5
x = 0.5
y = -0.5
z = 0.5

Apply bank +180 degrees: post multiply top row by i to give:

rightDown

heading = 0
attitude = 0
bank = 180 degrees

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =1
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0
s1 = sin(heading/2) =0
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =1

which gives:

w = 0
x = 1
y = 0
z = 0

backDown

heading = 90 degrees
attitude = 0
bank = 180 degrees

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0
s1 = sin(heading/2) =0.7071
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =1

which gives:

w = 0
x = 0.7071
y = 0
z = -0.7071

leftDown

heading = 180 degrees
attitude = 0
bank = 180 degrees

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0
s1 = sin(heading/2) =1
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =1

which gives:

w = 0
x = 0
y = 0
z = 1

forwardDown

heading = -90 degrees
attitude = 0
bank = 180 degrees

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0
s1 = sin(heading/2) =-0.7071
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =1

which gives:

w = 0
x = 0.7071
y = 0
z = 0.7071

Apply bank -90 degrees: post multiply top row by 0.7071 - i 0.7071 to give:

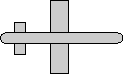
rightBack

heading = 0
attitude = 0
bank = -90 degrees

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =1
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0.7071
s1 = sin(heading/2) =0
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =-0.7071

which gives:

w = 0.7071
x = -0.7071
y = 0
z = 0

backLeft

heading = 90 degrees
attitude = 0
bank = -90 degrees

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0.7071
s1 = sin(heading/2) =0.7071
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =-0.7071

which gives:

w = 0.5
x = -0.5
y = 0.5
z = 0.5

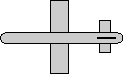
leftForward

heading = 180 degrees
attitude = 0
bank = -90 degrees

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0.7071
s1 = sin(heading/2) =1
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =-0.7071

which gives:

w = 0
x = 0
y = 0.7071
z = 0.7071

 

forwardRight

heading = -90 degrees
attitude = 0
bank = -90 degrees

w = c1 c2 c3 - s1 s2 s3
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

where:

c1 = cos(heading/2) =0.7071
c2 = cos(attitude/2) =1
c3 = cos(bank/2) =0.7071
s1 = sin(heading/2) =-0.7071
s2 = sin(attitude/2) =0
s3 = sin(bank/2) =-0.7071

which gives:

w = 0.5
x = -0.5
y = -0.5
z = -0.5
metadata block
see also:

 
Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.

cover us uk de jp fr caVisualizing Quaternions by Andrew J. Hanson

Other Math Books

Commercial Software Shop

Where I can, I have put links to Amazon for commercial software, not directly related to the software project, but related to the subject being discussed, click on the appropriate country flag to get more details of the software or to buy it from them.
cover Dark Basic Professional Edition - It is better to get this professional edition

cover This is a version of basic designed for building games, for example to rotate a cube you might do the following:
make object cube 1,100
for x=1 to 360
rotate object 1,x,x,0
next x

cover Game Programming with Darkbasic - book for above software

 

Can you help?

Please send me any improvements to here. I would appreciate ideas to make the pages more useful including error correction, ideas for new pages, improvements to wording. It helps if you quote the full URL of the page.

 

progam

I am working on a project which uses these principles, if you would like to help me with this you are welcome to join in, here:

http://sourceforge.net/projects/mjbworld/

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2008 Martin John Baker - All rights reserved - privacy policy.