Code

 public final void rotate(double heading, double attitude, double bank) {
	// Assuming the angles are in radians.
	double c1 = Math.cos(heading/2);
	double s1 = Math.sin(heading/2);
	double c2 = Math.cos(attitude/2);
	double s2 = Math.sin(attitude/2);
	double c3 = Math.cos(bank/2);
	double s3 = Math.sin(bank/2);
	double c1c2 = c1*c2;
	double s1s2 = s1*s2;
	w =c1c2*c3 - s1s2*s3;
	x =c1c2*s3 + s1s2*c3;
	y =s1*c2*c3 + c1*s2*s3;
	z =c1*s2*c3 - s1*c2*s3;
	angle = 2 * Math.acos(w);
	double norm = x*x+y*y+z*z;
	if (norm < 0.001) { // when all euler angles are zero angle =0 so
		// we can set axis to anything to avoid divide by zero
		x=1;
		y=z=0;
	} else {
		norm = Math.sqrt(norm);
    	x /= norm;
    	y /= norm;
    	z /= norm;
	}
}

Derivation of Equations

Start from quaternion to axis angle as shown here:

angle = 2 * acos(qw)
x = qx / sqrt(1-qw*qw)
y = qy / sqrt(1-qw*qw)
z = qz / sqrt(1-qw*qw)

Substitute from Euler to Quaternion as shown here:

qw = c1 c2 c3 - s1 s2 s3
qx = s1 s2 c3 +c1 c2 s3
qy = s1 c2 c3 + c1 s2 s3
qz = c1 s2 c3 - s1 c2 s3

where:

• c₁ = cos(heading / 2)
• c₂ = cos(attitude / 2)
• c₃ = cos(bank / 2)
• s₁ = sin(heading / 2)
• s₂ = sin(attitude / 2)
• s₃ = sin(bank / 2)

So, removing common factors which means that x,y,z is no longer normalised

angle = 2 * acos(c₁c₂c₃ - s₁s₂s₃)
x = s1 s2 c3 +c1 c2 s3
y = s1 c2 c3 + c1 s2 s3
z = c1 s2 c3 - s1 c2 s3

to normalise divide x,y and z by:

x² + y² + z² = (s1 s2 c3 +c1 c2 s3)²+(s1 c2 c3 + c1 s2 s3)²+(c1 s2 c3 - s1 c2 s3)²

Issues

• For issues concerning acos see here.
• Most trig functions (except openGL) use radians not degrees.

If you have a different result from that shown on this page it may be that you are using different standards, I have tried to keep the standards consistant accross this site and I have tried to define the standards that I am using here. One of these standards is that the order that the euler rotations are applied is 'NASA standard aeroplane' it uses a slightly different coordinate definition from VRML (z and y axis swapped). Also when working with aeroplanes we often work in terms of the position of external objects relative to the aircraft (i.e. the inverse of its position transform as explained here). therefore to get the expression normally used with NASA aeroplane we invert all inputs (change sign of every term with odd number of sine terms) invert output (conjugate quaternion) swap z and y for inputs (swap z and y columns) swap z and y for outputs (swap z and y rows). In the case of aircraft it can make sense to work in terms of the local frame of reference of the aircraft looking out, I have a version of this page that does that here, but be careful as this will no longer be compatible with the rest of this site.

However if you have checked these things and you still have a discrepency then I have probably made an error so please let me know here.

Example

we take the 90 degree rotation from this:

to this:

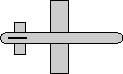As shown here the axis angle for this rotation is:

heading = 0 degrees
bank = 90 degrees
attitude = 0 degrees

• c₁ = cos(heading / 2) = 1
• c₂ = cos(attitude / 2) = 1
• c₃ = cos(bank / 2) = 0.7071
• s₁ = sin(heading / 2) = 0
• s₂ = sin(attitude / 2) = 0
• s₃ = sin(bank / 2) = 0.7071

angle = 2 * acos(c₁c₂c₃ + s₁s₂s₃) = 2 * acos(0.7071) = 90 degrees
x = c₁c₂s₃ - s₁s₂c₃ = 0.7071
y = c₁s₂c₃ + s₁c₂s₃ = 0
z = s₁c₂c₃ - c₁s₂s₃ = 0

So the axis is: (0.7071,0,0)

This can be normalised to: (1,0,0)

So this gives the correct result.

Angle Calculator and Further examples

I have put a java applet here which allows the values to be entered and the converted values shown along with a graphical representation of the orientation.

Also further examples in 90 degree steps here