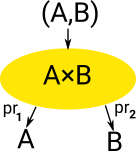
Product Type Has one constructor (formation) and multiple ways of deconstructing (elimination) (projections).
|
 |
Notation
In type theory the product of A and B is denoted A×B. In logic the product is 'and' often denoted /\ .
An element of A×B is denoted (a,b) where 'a' is an element of 'A' and 'b' is an element of 'B'.
Rules
Types are defined by their formation, term introduction, term eliminator and computation rules:
| Introduction | Elimination | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
This is discussed on the propositional logic page here.
In type theory types are defined in terms of:
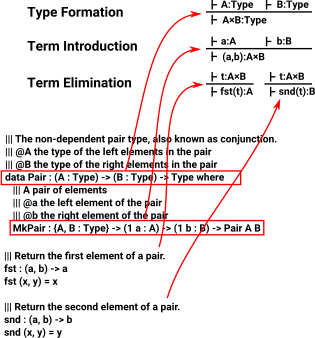
This picture shows how programming language constructs (In this case: Idris) relate to this theory: |
 |
β-reduction and η-reduction
β-reduction
construction followed by deconstruction:
- a = fst(a,b)
- b = snd(a,b)
η-reduction
deconstruction followed by construction:
- P = (fst P,snd P)
Implementations in Idris
Product terms can be defined using 'data' but there is also a specific mechanism for products using 'record'.
| Here we start with a product type 'M'. We can deconstruct it by using 'fst' and 'snd' then construct it to get back to 'M' | Idris> :let M = MkPair 2 "2" Idris> MkPair (fst M) (snd M) (2, "2") : (Integer, String) |
| Here we start with two terms 'x' and 'y' if we first construct using MkPair then deconstruct we get back to 'x' and 'y'. | Idris> :let x = 3 Idris> :let y = "3" Idris> fst (MkPair x y) 3 : Integer Idris> snd (MkPair x y) "3" : String |
Other implementations of product
Idris |
We can have a type which corresponds to conjunction:
|
|
from : Idris-dev/libs/prelude/Builtins.idr |
||| The non-dependent pair type, also known as conjunction.
||| @A the type of the left elements in the pair
||| @B the type of the right elements in the pair
data Pair : (A : Type) -> (B : Type) -> Type where
||| A pair of elements
||| @a the left element of the pair
||| @b the right element of the pair
MkPair : {A, B : Type} -> (1 a : A) -> (1 b : B) -> Pair A B |
|
| from : Idris-dev/libs/prelude/ Prelude/Basics.idr | ||| Return the first element of a pair. fst : (a, b) -> a fst (x, y) = x ||| Return the second element of a pair. snd : (a, b) -> b snd (x, y) = y |
|
|
from : coq/theories/Init/Datatypes.v |
(** [prod A B], written [A * B], is the product of [A] and [B];
the pair [pair A B a b] of [a] and [b] is abbreviated [(a,b)] *)
#[universes(template)]
Inductive prod (A B:Type) : Type :=
pair : A -> B -> A * B
where "x * y" := (prod x y) : type_scope.
Add Printing Let prod.
Notation "( x , y , .. , z )" := (pair .. (pair x y) .. z) : core_scope.
Arguments pair {A B} _ _.
Register prod as core.prod.type.
Register pair as core.prod.intro.
Register prod_rect as core.prod.rect.
Section projections.
Context {A : Type} {B : Type}.
Definition fst (p:A * B) := match p with (x, y) => x end.
Definition snd (p:A * B) := match p with (x, y) => y end.
Register fst as core.prod.proj1.
Register snd as core.prod.proj2.
End projections. |
Logic
In logic the product is 'and' denoted /\
Relationship to Category Theory
Category theory is deeply related to type theory.
On this page is product is approached from the category theory direction and on this page is generalsed to the concept of a limit.
Next Steps
Other types are discussed on the following pages: