Vector Division
Neither dot or cross vector multiplication have a unique inverse.
In the case of dot multiplication this converts from vector to scalar which looses information so it does not have an inverse.
In the case of cross multiplication there are many values of the vector B which will generate the result A x B so division does not give a unique value. The blue vectors in the diagram below shows some vectors that produce the same product as vector B.
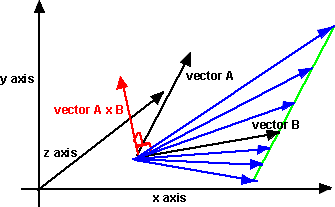
Given the direction of any potential inverse B' we can determine its length:
since: |A x B| = |A| *|B'| * sin(θ)
so: |B'| = |A x B| / ( |A| * sin(θ))
Thanks to Paolo De Leva for correcting this.
inverse of cross multiplication using triple product identity
If A,B and C are vectors and x is cross multiplication, then,
if
C = B x A
can we solve this for B? Start with A x C and substitute equation above gives,
A x C = A x (B x A)
Using the vector triple product identity gives
A x C = B (A·A) - A (A·B)
B (A·A) = A x C + A (A·B)
A·A = | A |2 (for example if A is dimension 3 then A·A = a.x2 + a.y2 + a.z2)
B = (A x C + A (A·B))/| A |2
can't quite eliminate B of right hand side unless A and B are mutually perpendicular in which case A·B = 0 and the equation can be solved:
if C = B x A also B and A are mutually perpendicular, then: B = (A x C)/| A |2
Thank you to Mati Meron for explaining this to me in the context of rotation dynamics.
Attempt to find inverse of cross multiplication using skew symmetric matrix
We can convert the vector equation into a 3x3 skew symmetric matrix expression and then invert the matrix. So if:
C = A x B
We want to get an expression for B in terms of A and C. So first we rewrite the expression in terms of a skew symmetric matrix [~A] such that:
C = [~A] B
This matrix is:
| [~A] = |
|
As described here.
B = [~A]-1 C
This inverse matrix will be
| [~A] =1/det[m] * |
|
where det = Ay*Az*Ax -Az*Ax*Ay = 0
So all terms go to 1/0 = infinity, I think this confirms that there is no inverse of the 'x', not because of any deficiency with vector notation, but because of what we are trying to model. In other words there are many vectors which, when multiplied together, will produce a given result.
Inverse Vector using Geometric Multiplication
Although cross multiplication and dot multiplication don't have an inverse for the reasons discussed, there is a different type of multiplication that does have an inverse for vectors. (as pointed out on web forum)
This is Clifford Algebra/Geometric Algebra as described here. The interpretation of this type of multiplication is different, its not concerned with mutually perpendicular vectors, although geometric multiplication can be thought of as a combination of cross and dot multiplication.
We want to find the inverse of the vector 'a' which is equivalent to solving the equation:
a-1 a = 1
To solve this equation we can use the property that, in geometric algebra, the square of a vector is a scalar, so,
a2 = |a|2
Combining these gives:
a-1 = a /|a|2


