Maths - Simultaneous equations

In the last section we looked at functions of one variable, in this section we are looking at functions of more than one variable, usually denoted x, y, z.

If we have one equation with one unknown then, in many cases, we can solve it. If we have two unknowns then we need at least 2 equations which apply to the same two unknowns.

For example, perhaps we know by some means that:

2x + 3y = 13

and at the same time we also know that:

4x + y = 11

Then we can calculate the values of x and y. There are several ways to do this, perhaps the most straightforward is by substituting one equation in the other. For instance from the second we can get:

y = 11 - 4x

We can now substitute this in the first to give:

2x + 3*(11 - 4x) = 13

multiplying out the terms gives:

2x + 33 - 12x = 13

20 = 10x

so x =2

We can then substitute this back into either equation, say:

4*2 + y = 11

so

y=3

and we have found the two variables x =2 and y=3.

Graphical Methods

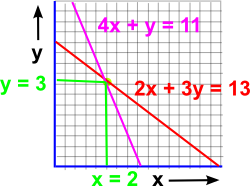	In this case, where we have two dimensions x and y, we can show the two equations as lines. The solution is then the point where the two lines meet.
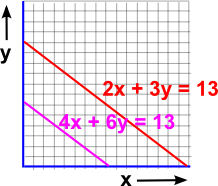	The graphical approach also allows us to visualize what happens when there is no solution. For instance, if both the equations are the same, then the lines overlap and all points on the line are solutions. Alternatively if the lines are different but parallel then they do not meet and there is no solution. Or we could say that the lines meet at infinity, in which case there are two solutions at x= +∞, y= -∞ and x= -∞, y= +∞ (but not at x= +∞, y= +∞ and x= -∞, y= - ∞).
	If we move up to 3 equations in 3 unknowns then each equation like: 2x + 3y - 4z = 8 Then we might guess that the equation might represent a line through a 3 dimensional volume, but this is not quite the case, in fact it represents a plane through the 3D volume. Again if the 3 planes are all independent, not parallel, then there will be a unique solution.
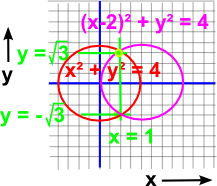	We can also use graphical methods to give insight to simultaneous non-linear equations. For example: x²+y²=4 (x-2)²+y²=4 have two possible solutions (1,√3) and (1,-√3).
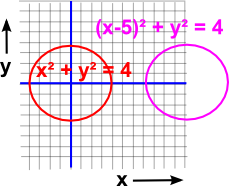	By the 'continuity principle' if we change the second equation to (x-5)²+y²=4 then there will still be two solutions even though the diagram shows no intersection. However there is only a solution in the field of complex numbers at (5/2, 3/2 i ) and (5/2, -3/2 i ).

So from this we can see that each equation may constrain the solution further until we get a unique solution.

Linear Functions

As explained on the polynomial page, there are two ways to define linear functions, some definitions allow a constant offset and some don't.

f(x) = a * x + b

or

f(x) = a * x

The second definition is an example of a linear map or linear operator. We can extend this for several variables:

f1(x,y) = a0 * x + a1 * y
f2(x,y) = a2 * x + a3 * y

This can be represented with vectors and matrices:

as explained on these pages.

Bilinear Functions

A Bilinear function is a function of two variables which is linear when each variable is taken on its own (making the other variables constant).

A linear function could be represented like this:

f(x) = a * x

where:

• a = constant
• x = variable

So a bilinear function could be represented like this:

B(x,y) = x * y

because if x and y are made constant, in turn, then the equation is linear (like f(x) above).

This appears so simple that its hardly worth using a special name for it, however, when we are working with quantities made up of several scalars such as vectors then it becomes useful to define the properties of such functions.

A more mathematical way to define a bilinear operator in terms of vector spaces:

B: V x W -> X

where:

• B is the bilinear operator being defined
• V, W and X are vector spaces over the same field F

Which has the property of being linear when each variable is taken on its own (making the other variables constant).

A special case is the 'bilinear form', where X is the complete field F.

The following applies for the bilinear form:

for any a,b and c in V & W:

B(fa+b,c) = f B(a,c) + B(b,c)
B(a,f b + c) = f B(a,b) + B(a,c)

Possible additional assumptions:

• symmetric: B(x,y) = B(y,x)
• antisymmetric: B(x,y) = -B(y,x)
• alternating: B(x,x) = 0

See also quadratic form.

Examples:

The bilinear operator can be used to analyse different types of multiplication, for example:

matrix multiplication

Is a bilinear map: M(m,n) x M(n,p) -> M(m,p)

x₀₀ = v ₀₀*w₀₀ + v ₀₁*w₁₀

x₀₁= v ₀₀*w₀₁ + v ₀₁*w₁₁

x₁₀ = v ₁₀*w₀₀+ v ₁₁*w₁₀

x₁₁ = v ₁₀*w₀₁ + v ₁₁*w₁₁

The dot product

Is a bilinear operator V x V -> F

x = v₀ * w₀ + v₁ * w₁ + v₂ * w₂

The cross product

In R3 is a bilinear operator R3 x R3 -> R3

x₀ = v₁ * w₂ - w₁ * v₂
x₁ = v₂ * w₀ - w₂ * v₀
x₂ = v₀ * w₁ - w₀ * v₁

Quaternions

So is quaternion multiplication bilinear? the equations for multiplication are:

x₀ = v₀*w₀ - v₁*w₁ - v₂*w₂- v₃*w₃

x₁ = v₁*w₀ + v₀*w₁ + v₂*w₃ - v₃*w₂

x₂ = v₀*w₂ - v₁*w₃ + v₂*w₀ + v₃*w₁

x₃ = v₀*w₃ + v₁*w₂ - v₂*w₁ + v₃*w₀

When we are using quaternions for transforms we use two multiplications, P2=q * P1 * q', can we represent this as a bilinear function:

x₀ = v₃*v₃*w₀ + 2*v₁*v₃*w₂ - 2*v₂*v₃*w₁ + v₀*v₀*w₀ + 2*v₁*v₀*w₁ + 2*v₂*v₀*w₂ - v₂*v₂*w₀ - v₁*v₁*w₀
x₁ = 2*v₀*v₁*w₀ + v₁*v₁*w₁ + 2*v₂*v₁*w₂ + 2*v₃*v₂*w₀ - v₂*v₂*w₁ + v₃*v₃*w₁ - 2*v₀*v₃*w₂ - v₀*v₀*w₁
x₂ = 2*v₀*v₂*w₀ + 2*v₁*v₂*w₁ + v₂*v₂*w₂ - 2*v₃*v₁*w₀ - v₁*v₁*w₂ + 2*v₃*v₀*w₁ - v₀*v₀*w₂ + v₃*v₃*w₂

Simultaneous Quadratic Equations

One linear and one quadratic

Using the linear expression express one unknown in terms of the other and then substitute in the quadratic. This will give a quadratic with one variable only, which is solved in the usual way, then the other variable can be found by substitution as for linear simultaneous equations.

Example 1

(1) 4x + 5y = 0
(2) 2 x² + y x - y² = 14

from (1) x = -(5/4)y

substitute in (2)

2 (-5/4 y)² + (-5/4 y) y - y ² = 14

(25/8) y² - (5/4) y² - y ² = 14

25 y² - 10 y² - 8 y ² = 112

7 y² = 112

y = ±√112/7

y = ±√16

y = ±4

now substitute in (1)

4x + 5(±4) = 0

4x = ±20

x = ±5

Example 2

(1) x - y = 1
(2) x² + y² = 61

x = y + 1

(y + 1)² + y² = 61

y² + 2y + 1 = 61

y² + 2y - 60 = 0

y = (-2 ±√(22))/2

y = -6 or 5

x = -5 or 6

Simultaneous Equations Involving Three Unknowns

The currents x,y,z amps in a circuit are given by the following equations, find the currents:

(1) 3x + 2y - 2z = 16
(2) 4x + 3y + 3z = 2
(3) -2x + y - z = 1

To eliminate z from (1) & (2) multiply (1)*3 & (2)*2 to give:

9x + 6y - 6z = 48
8x + 6y + 6z = 2

Subtracting these equations gives:

(4) 17x + 12y = 52

To eliminate z from (2) & (3) multiply (3)*3 to give:

4x + 3y + 3z = 2
-6x + 3y - 3z = 3

Subtracting these equations gives:

(5) -2x + 6y = 5

x can be found from (4) & (5)*2

17x + 12y = 52
-4x + 12y = 10

Subtracting gives:

x = 42/21

x = 2

substitute in (4) gives:

34 + 12 y = 52

y = 18/12

y = 1.5

substitute these values for x and y in (1)

6 + 3 - 2z = 16

-2z = 7

z = -7/2

z = -3.5

Program

There are a number of open source programs that can solve simultaneous equations. I have used Axiom, how to install Axiom here.

To get a numeric solution for a given system of equations, we can use solve as shown here:

solve([x + 2*y = 5, 3*x + 4*y = 6],[x, y])

I have put user input in red:

(1) -> solve([x + 2*y = 5, 3*x + 4*y = 6],[x, y])

                    9
   (1)  [[x= - 4,y= -]]
                    2
   Type: List List Equation Fraction Polynomial Integer
(2) ->

Or we can find a general formula for a system of 2 linear equations using solve as shown here:

(1) -> solve([a*x + b*y = e, c*x + d*y = f],[x, y])

 UserDefinedPartialOrdering
          - b f + d e    a f - c e
(1)  [[x= -----------,y= ---------]]
           a d - b c     a d - b c
         Type: List List Equation Fraction Polynomial Integer
(2) ->

Or we can do the same thing using matrix algebra:

(1) -> solve(matrix([[a, b], [c, d]]),[e, f])

      UserDefinedPartialOrdering
                      - b f + d e a f - c e
   (1)  [particular= [-----------,---------],basis= [[0,0]]]
                       a d - b c  a d - b c

   Type: Record(particular: 
       Union(Vector Fraction Polynomial Integer,"failed")

,basis: List Vector Fraction Polynomial Integer)
(2) ->

Next

see unifier page

EuclideanSpace

home

Linear Functions

Open Source Algebra Programs

Problem Solving

Bilinear and Quadratic Forms