By: nobody ( Nobody/Anonymous ) |
When building particle
engines you want the emitter to expell particles with a certain range
of velocity. Restraints on the direction ther are expeled are given by
a direction and an angle. |
By: martinbaker
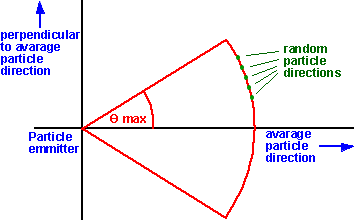
Can I first check if I have understood correctly by taking the simpler 2 dimensional case.
So how do we define the velocity distribution? I can think of the following possibilities:
- magnitude fixed, direction evenly distributed on circle - It seems to me that this is equivalent to choosing a random angle between theta and -theta. I guess this might happen if watering the garden with some sort of diffuser attached to the hose.
- Magnitude fixed, perpendicular direction evenly distributed - so sin(theta) = perpendicular/radius. This would seem to apply where say, a jet of water is being sprayed in one direction, but random collisions are generating some velocity component perpendicular to hose.
- Magnitude and direction variable, direction as in 1 or 2. Magnitude is a random number between 0 and vmax.
- Magnitude and direction variable, direction as in 1 or 2. Magnitude is a random number between vmin and vmax. I guess this might happen where all particles start out with velocity vAverage but due to random events the velocity range expands between vmin and vmax.
- Magnitude and direction variable, values are evenly distributed within the bounds of the red line above. I guess this could be generated by taking random points on plane between -xmax and xmax and between -ymax and ymax, then rejecting all points which lie outside red line.
As you suggest, I suspect that real physics examples would give more of a bell shaped distribution.
Martin
By: nobody ( Nobody/Anonymous ) |
Exactly as I thought
of it. Anyways here is my solutions which may be flawed but appears to
work well. I took functions for uniformly ditributing points on a sphere
from wolfram site and started fooling with them. |
By: nobody ( Nobody/Anonymous ) |
Here is also a the
link I am using to the Wolfram site: |