To define rules we need a base type and expressions defined in that type. The base type and the expressions require the following:
Rules must be defined in terms of a category with:
in turn FunctionSpace requires:
|
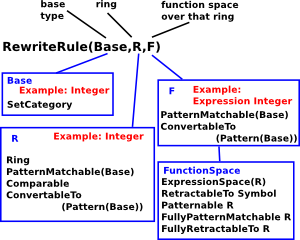 |
That is, the left and right hand side of the equation must extend these.
For example: Expression(R) extends FunctionSpace(R).
Interpreter Syntax for Rules
The interpreter seems to have a special syntax for entering rules:
(1) -> R1 := rule log(x) + log(y) == log(x*y)
(1) log(y) + log(x) + %B == log(x y) + %B
Type: RewriteRule(Integer,Integer,Expression(Integer)) |
The simplest form of this special syntax is something like:
'rule' expression '==' expression
but there are more complicated versions like:
'rule' var | predicate var '==' expression
Multiple rules can be entered to a ruleset by using indentation.
I tried doing the same thing, without using this special syntax, I could not get this to work:
(3) -> E1 := log(x) + log(y)
(3) log(y) + log(x)
Type: Expression(Integer)
(4) -> E2 := log(x*y)
(4) log(x y)
Type: Expression(Integer)
(5) -> RR := RewriteRule(Integer,Integer,Expression(Integer))
(5) RewriteRule(Integer,Integer,Expression(Integer))
Type: Type
(6) -> R1 := rule(E1,E2)$RR
Line 1: R1 := rule(E1,E2)$RR
.............A
Error A: syntax error at top level
Error A: Improper syntax.
2 error(s) parsing
|
Why does that not work? I would have thought it would work according to this:
(2) -> )show RewriteRule RewriteRule(Base: SetCategory,R: Join(Ring,PatternMatchable(Base),Comparable, ConvertibleTo(Pattern(Base))),F: Join(FunctionSpace(R),PatternMatchable(Base), ConvertibleTo(Pattern(Base)))) is a domain constructor Abbreviation for RewriteRule is RULE This constructor is exposed in this frame. ------------------------------- Operations -------------------------------- ?=? : (%,%) -> Boolean coerce : Equation(F) -> % coerce : % -> OutputForm elt : (%,F,PositiveInteger) -> F ?.? : (%,F) -> F hash : % -> SingleInteger latex : % -> String lhs : % -> F pattern : % -> Pattern(Base) retract : % -> Equation(F) rhs : % -> F rule : (F,F,List(Symbol)) -> % rule : (F,F) -> % ?~=? : (%,%) -> Boolean hashUpdate! : (HashState,%) -> HashState quotedOperators : % -> List(Symbol) retractIfCan : % -> Union(Equation(F),"failed") suchThat : (%,List(Symbol),(List(F) -> Boolean)) -> % |
This appears to work, but I don't think it does because E1 and E2 are taken as, variables in the rule, rather than expressions?
(6) -> R1 := rule E1 == E2
(6) E1 == E2
Type: RewriteRule(Integer,Integer,Expression(Integer)) |
Applying the Rules
This is not what I expected:
(7) -> E3 := log(sin(x))+log(y)
(7) log(sin(x)) + log(y)
Type: Expression(Integer)
(8) -> R1 E3
(8) E2
Type: Expression(Integer)
(9) -> R1 log(sin(x))+log(y)
(9) log(y) + E2
Type: Expression(Integer) |
(6) -> )di op rule
There are 2 exposed functions called rule :
[1] (D1,D1,List(Symbol)) -> RewriteRule(D3,D4,D1)
from RewriteRule(D3,D4,D1)
if D3 has SETCAT and D4 has Join(Ring,PatternMatchable(D3),
Comparable,ConvertibleTo(Pattern(D3))) and D1 has Join(
FunctionSpace(D4),PatternMatchable(D3),ConvertibleTo(
Pattern(D3)))
[2] (D1,D1) -> RewriteRule(D2,D3,D1) from RewriteRule(D2,D3,D1)
if D2 has SETCAT and D3 has Join(Ring,PatternMatchable(D2),
Comparable,ConvertibleTo(Pattern(D2))) and D1 has Join(
FunctionSpace(D3),PatternMatchable(D2),ConvertibleTo(
Pattern(D2))) |
see:
- pattern.spad.pamphlet
- patmatch1.spad.pamphlet
- patmatch2.spad.pamphlet
- rule.spad.pamphlet
(1) -> PMR := PatternMatchResult(Integer, Symbol)
(1) PatternMatchResult(Integer,Symbol)
Type: Type
(2) -> P := Pattern(Integer)
(2) Pattern(Integer)
Type: Type
(3) -> p := (1$Integer) :: P
(3) 1
Type: Pattern(Integer)
(4) -> pmr := new()$PMR
(4) []
Type: PatternMatchResult(Integer,Symbol)
(5) -> patternMatch("*"::Symbol,p,pmr)$Symbol
(5) Does not match
Type: PatternMatchResult(Integer,Symbol)
|
Further Topics
Can we use this pattern matching mechanism for matching types (type inference) in the interpreter? See dicussion on page here.