This is part of some experimental code that I am writing to implement the FriCAS interpreter using SPAD code. For an overview of this experiment see page here. For information about how this is done using the current boot/lisp code see the page here.
The previous stage (the parser) has generated an atomic value tree (which is as close as we get in SPAD to untyped since SPAD uses static typing) . Here we need to add higher level SPAD types to the tree. If the types are explicitly declared, then this is easy , but otherwise we need to infer the types.
| In this case we have an operator '=' where we know it input types (Integer) and output type (Boolean) so we know which '=' to use. | |
| Even if we don't know all the input and output types we may be able to infer it if there is only one function signature that matches. | |
| This gets more complicated when an unknown type needs to match an input for one function and an output for another. | 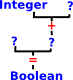 |
Atomic Value Tree
The previous stage generated an atomic value tree, it has a format like this:
 |
Here leaves are atomic types which are one of:
Nodes are one of:
|
When parsing input it will only have 1 element of a union so, at this stage we wont necessarily see unions. Also records and unions wont necessarily have selector values.
The concept is similar to lisp SExpressions but I have used this instead to avoid reliance on building on top of lisp. Lisp builds tree structures by having lists whose elements may possibly be lists, whereas here we are using an explicit tree structure.
So this allows us to hold a value in terms of atomic types (which is as close as we get to being untyped). We now want to map this to higher level types (SPAD domains).
Pattern Match
In order to infer the higher level SPAD types we try each domain in turn, starting with the largest and most complex, if they fail to match then we try simpler types until we do get a match.
We can get information about functions/operations from databases as described on page here.
We then need to pattern match this. There is a mechanism in SPAD for pattern matching, in ordinary expressions, which is used in specifying rewrite rules. Is there an way that we can use that mechanism, not for an expression on ordinary functions, but for a 'type expression'? that is an expression where all the 'values' are 'types'.
There is more information about this SPAD pattern matching mechanism on page here.
I have therefore written a domain 'MatchableType' (more details here) which implements:
- ConvertibleTo(Pattern(MatchableType))
- PatternMatchable(MatchableType)
This can represent types as follows:
(2) -> A := mType("Integer"::Symbol)
(2) Integer
Type: MatchableType
(3) -> B := mType("Symbol"::Symbol)
(3) Symbol
Type: MatchableType
(4) -> C := mType("Record"::Symbol,[A,B])
(4) Record(Integer,Symbol)
Type: MatchableType |
Issues with Pattern Match
I'm not sure if it is a good idea to use the Axiom/FriCAS built-in pattern match system or not? We need to create:
- MType - A matchable type domain
- MTypeExpression - An extension of Expression which can represent types in Expression
Issues are:
- We need to have symbols to represent fixed types like 'Integer' and 'Float' type constructors () like 'List' and also variables that can stand for variables that can stand for any types.
- Output form of Expression (which uses Output form of SparseMultivariatePolynomial) uses a particular format (like space for *) which may not be appropriate for what we want.
InputForm
This is defined in: mkfunc.spad.pamphlet
Any domain can control how it is parsed by defining:
convert(%) : InputForm
++ Domain of parsed forms which can be passed to the interpreter.
++ This is also the interface between algebra code and facilities
++ in the interpreter.
InputForm():
Join(SExpressionCategory(String, Symbol, Integer, DoubleFloat),
ConvertibleTo SExpression) with
interpret : % -> Any
++ interpret(f) passes f to the interpreter.
convert : SExpression -> %
++ convert(s) makes s into an input form.
binary : (%, List %) -> %
++ \spad{binary(op, [a1, ..., an])} returns the input form
++ corresponding to \spad{a1 op a2 op ... op an}.
function : (%, List Symbol, Symbol) -> %
++ \spad{function(code, [x1, ..., xn], f)} returns the input form
++ corresponding to \spad{f(x1, ..., xn) == code}.
lambda : (%, List Symbol) -> %
++ \spad{lambda(code, [x1, ..., xn])} returns the input form
++ corresponding to \spad{(x1, ..., xn) +-> code} if \spad{n > 1},
++ or to \spad{x1 +-> code} if \spad{n = 1}.
"+" : (%, %) -> %
++ \spad{a + b} returns the input form corresponding to \spad{a + b}.
"*" : (%, %) -> %
++ \spad{a * b} returns the input form corresponding to \spad{a * b}.
"/" : (%, %) -> %
++ \spad{a / b} returns the input form corresponding to \spad{a / b}.
"^" : (%, NonNegativeInteger) -> %
++ \spad{a ^ b} returns the input form corresponding to \spad{a ^ b}.
"^" : (%, Integer) -> %
++ \spad{a ^ b} returns the input form corresponding to \spad{a ^ b}.
0 : constant -> %
++ \spad{0} returns the input form corresponding to 0.
1 : constant -> %
++ \spad{1} returns the input form corresponding to 1.
flatten : % -> %
++ flatten(s) returns an input form corresponding to s with
++ all the nested operations flattened to triples using new
++ local variables.
++ If s is a piece of code, this speeds up
++ the compilation tremendously later on.
unparse : % -> String
++ unparse(f) returns a string s such that the parser
++ would transform s to f.
++ Error: if f is not the parsed form of a string.
parse : String -> %
++ parse(s) is the inverse of unparse. It parses a
++ string to InputForm
declare : List % -> Symbol
++ declare(t) returns a name f such that f has been
++ declared to the interpreter to be of type t, but has
++ not been assigned a value yet.
++ Note: t should be created as \spad{devaluate(T)$Lisp} where T is the
++ actual type of f (this hack is required for the case where
++ T is a mapping type).
compile : (Symbol, List %) -> Symbol
++ \spad{compile(f, [t1, ..., tn])} forces the interpreter to compile
++ the function f with signature \spad{(t1, ..., tn) -> ?}.
++ returns the symbol f if successful.
++ Error: if f was not defined beforehand in the interpreter,
++ or if the ti's are not valid types, or if the compiler fails. |
Next step
The output of this parser is passed on to the evaluator as described on the page here.