The interpreter code is written in a language called 'boot' which is part way between Lisp and SPAD (more information about boot on this page). I would like to be able to translate this code to from boot to SPAD and I have started a project described here.
The SPAD interpreter reads in a line (or lines) of text and converts this to a tree structure, the SPAD types are inferred, any actions such as assignments are carried out and the result is formatted and output to the formatter. This is very complex and there is a lot of other things going on like macro expansion, interaction with databases, pattern matching, interaction with inputForm and outputForm of domains etc.
In the SPAD interpreter these stages are not completely separate but, to try to understand it, I am trying to approximate to some form of top level structure.
These diagrams are far from correct but I have to start somewhere: This diagram is my first attempt to try to capture the various forms that the input goes through as it is parsed. System commands, starting with ')', don't go through this route. Below I have tried to indicate some of the main functions that do these transforms. This picture is complicated somewhat by the experimental nature of part of the interpreter. |
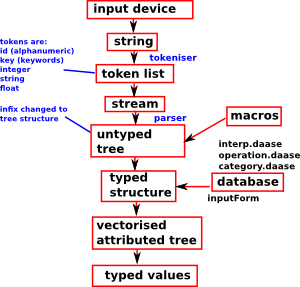 |
Tokeniser
This takes the input string and converts it to a list of tokens. In the case of the SPAD interpreter, the tokentiser is not really separated out as a separate entity since it is mixed up with the zipper structure described in the parser section below.
The token types are:
- id - identifier
- key - key word
- integer
- rinteger - what is 'rinteger' ?
- float - float token seems to have special issues.
- string
- comment
- negcomment
- error
- spaces
The keywords are:
| add,add | and , and | break , break |
| by , by | case , case | catch , catch |
| default , DEFAULT | define , DEFN | do , DO |
| else , else | exquo , exquo | export , EXPORT |
| finally , finally | for , for | free , FREE |
| from , from | generate , generate | goto , goto |
| has , has | ||
| if , if | import , import | in , in |
| inline , INLINE | is , is | isnt , isnt |
| iterate , ITERATE | local , local | macro , MACRO |
| mod , MOD | not , not | or , or |
| pretend , pretend | quo , quo | rem , rem |
| repeat , repeat | return , return | rule , RULE |
| then , then | try , try | until , until |
| where , where | while , while | with , with |
| yield , yield | | , BAR | ". , DOT |
| :: , COERCE | : , COLON | :- , COLONDASH |
| @ , AT | @@ , ATAT | , , COMMA |
| ; , SEMICOLON | ** , POWER | * , TIMES |
| + , PLUS | - , MINUS | < , LT |
| > , GT | <= , LE" | >= , GE |
| = , EQUAL | ~= , NOTEQUAL | ~ , ~ |
| ^ , CARAT | .. , SEG | # , # |
| #1 , #1 | & , AMPERSAND | $ , $ |
| / , SLASH | \ , BACKSLASH | // , SLASHSLASH |
| \\ , BACKSLASHBACKSLASH | /\ , SLASHBACKSLASH | \/ , BACKSLASHSLASH |
| => , EXIT | := , BECOMES | == , DEF |
| ==> , MDEF | -> , ARROW | <- , LARROW |
| +-> , GIVES | ( , ( | ) , ) |
| (| , (| | |) , |) | [ , [ |
| ] , ] | [__] , [] | { , { |
| } , } | {__} , {} | [| , [| |
| |] , |] | [|__|] , [||] | {| , {| |
| |} , |} | {|__|} , {||} | << , OANGLE |
| >> , CANGLE | "' , '" | ` , BACKQUOTE |
Its a bit difficult to analyise the tokeniser for the interpreter. Not only is it largely undocumented (as expected) but it is also mixed up with the complicated zipper mechanism discussed in the parser section below.
scan.boot
This does the low level tokenising
lineoftoks
Bites off a token-dq from a line-stream returning the token-dq and the rest of the line-stream:
| As an example we tokenise "a+2". We first use incString to produce the right structure to apply to lineoftoks which does the tokenising. | (1) -> a := incString("a+2")$Lisp
(1)
(nonnullstream # |
Parser
The parser converts a list of tokens to a tree structure.
| So a list of tokens like 2*(3+4) would be converted to a structure like: | 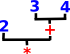 |
The code for this uses complicated recursive techniques. Of course these expressions are naturally recursively defined but the code goes to the extent of using a 'zipper' structure. I get the impression that this is intended to traverse the structure in a non mutable way without having any pointers.
In a very interesting e-mail conversation Tim Daly explained some of the background:
| "Bill Burge was interested in recursive techniques and decided to write a recursive parser. It was "interesting" and not the way you would expect a parser to be written but, as long as it sorta-kinda worked nobody cared. The whole IBM team was made up of really creative people, each working on their own ideas. Things broke all the time since we were constantly changing things. The syntax really did change on a weekly basis." |
and
"Bill Burge was our "language" guy who was the primary author of the Spad and BOOT parsers. His area of research was recursive programming techniques, hence the "zipper parser" in Axiom. (W.H. Burge "Recursive Programming Techniques" ISBN 0201144506) Once a week there was a new (new-new-new...) parser from Bill. (This became an "in-group" joke as in "are we running the NEW parser?")" |
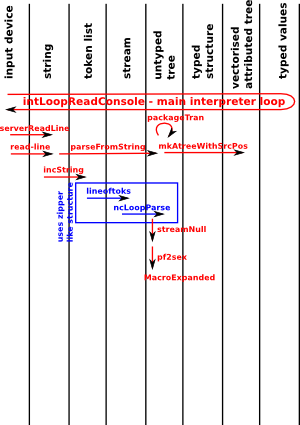
int-top.boot
The main interpreter loop seems to be in int-top.boot:
intloopReadConsole
This reads a complete line, upto carriage return from stdin or other input source. Detects system commands, line starting with ')'. If not a system command then it attempts to parse.
I found the simplest way to read a line from SPAD is this:
a := read_-line(_*STANDARD_-INPUT_*$Lisp)$Lisp
s:String := a pretend String |
Of course, as it stands it only handles input from stdin. We need to handle input from other sources and continued lines etc.
incString
The tokeniser needs to start with a certain structure so 'incString' is first called to put in that structure:
(1) -> incString("a+2")$Lisp
(1)
(nonnullstream # |
| intLoopReadConsole | This is the top level loop when reading from the input console. This function calls itself after processing the current line. Because of this it is important that the underlying common lisp supports tail-recursion. Normally we never really exit this function. |
cstream.boot
The first stage of parsing seems to be done in cstream.
As explained in vol5:
The input stream is parsed into a large s-expression by repeated calls This delay structure is given to StreamNull which walks along the So, in effect, the input is "zipped up" into a Delay data structure |
When implementing this in SPAD do we really need to replicate this zipper data structure? Is it used just to avoid having a mutable data structure? If so, mutable data may be preferable to all this complexity and recursion?
Would it be easier to implement an instance of category LZSTAGG LazyStreamAggregate? So we construct the stream with the string we want to tokenise then we can just keep calling 'frst' and 'rst' to get next token?
next
:
fricas / src / interp / i-toplev.boot
read-line |
(1) -> a := read_-line(_*STANDARD_-INPUT_*$Lisp)$Lisp
hello
(1) hello
Type: SExpression |
serverReadLine This reads in a line of text upto carrage-return from the curinstream variable which is set by *standard-input* common lisp variable. |
(1) -> a:= serverReadLine(_*STANDARD_-INPUT_*$Lisp)$Lisp
hello
(1) hello
Type: SExpression
(2) -> a
(2) hello
Type: SExpression
|
processInteractive |
(7) -> processInteractive(parseFromString("2*3.4")$Lisp,nil)$Lisp
(7) 6.8
Type: Float
|
interpretTopLevel(parseFromString("2*3.4")$Lisp,nil)$Lisp
(9) ((Float) WRAPPED 250875719402449901978 . - 65)
Type: SExpression |
fricas / src / interp / i-syscmd.boot
'parseFromString' is called to take user input and convert it into an SExpression. This parses into an SExpression like (+ 1 2) but it is not evaluated to give 3. To actually do the evaluation we would need to call 'processInteractive'. (see: i-toplev.boot). |
(1) -> parseFromString("1+2")$Lisp
(1) (+ 1 2)
Type: SExpression
(2) -> parseFromString("1")$Lisp
(2) 1
Type: SExpression
(3) -> parseFromString("a")$Lisp
(3) a
Type: SExpression
(4) -> parseFromString("1.2")$Lisp
(4) (($elt (Float) float) 12 - 1 10)
Type: SExpression
(5) -> parseFromString("%a")$Lisp
(5) %a
Type: SExpression
(5) -> parseFromString("2*3.4")$Lisp
(5) (* 2 (($elt (Float) float) 34 - 1 10))
Type: SExpression |
g-util.boot
'packageTran' parseFromString is usually composed with 'packageTran' although packageTran does not seem to do anything. |
(6) -> packageTran(parseFromString("2*3.4")$Lisp)$Lisp
(6) (* 2 (($elt (Float) float) 34 - 1 10))
Type: SExpression |
fricas / src / interp / i-intern.boot
Internal Interpreter Facilities
Vectorized Attributed Trees
The interpreter translates parse forms into vats for analysis.
These contain a number of slots in each node for information.
The leaves are now all vectors, though the leaves for basic types
such as integers and strings used to just be the objects themselves.
The vectors for the leaves with such constants now have the value
of $immediateDataSymbol as their name. Their are may still be
some functions that still check whether a leaf is a constant. Note
that if it is not a vector it is a subtree.
attributed tree nodes have the following form:
| slot | description |
| 0 | operation name or literal |
| 1 | declared mode (type?) of variable |
| 2 | computed value of subtree from this node |
| 3 | modeset: list of single computed mode of subtree |
| 4 | prop list for extra things |
mkAtreeWithSrcPos
| mkAtreeWithSrcPos | (10) -> mkAtreeWithSrcPos(parseFromString("2*3.4")$Lisp,nil)$Lisp
(10)
([*,NIL,NIL,NIL,NIL] [--immediateData--,NIL,PositiveInteger()(),NIL,NIL]
([Dollar,NIL,NIL,NIL,NIL] (Float)
([float,NIL,NIL,NIL,NIL]
[--immediateData--,NIL,PositiveInteger()(),NIL,NIL]
[--immediateData--,NIL,Integer()(),NIL,NIL]
[--immediateData--,NIL,PositiveInteger()(),NIL,NIL])
)
)
Type: SExpression |
fricas / src / interp / i-eval.boot
(1) -> a := mkAtreeWithSrcPos(parseFromString("2*3.4")$Lisp,nil)$Lisp
(1)
([*,NIL,NIL,NIL,NIL] [--immediateData--,NIL,PositiveInteger()(),NIL,NIL]
([Dollar,NIL,NIL,NIL,NIL] (Float)
([float,NIL,NIL,NIL,NIL]
[--immediateData--,NIL,PositiveInteger()(),NIL,NIL]
[--immediateData--,NIL,Integer()(),NIL,NIL]
[--immediateData--,NIL,PositiveInteger()(),NIL,NIL])
)
)
Type: SExpression
(2) -> v := getValue(a)$Lisp
(2) ()
Type: SExpression
(3) -> om := objMode(v)$Lisp
(3) ()
Type: SExpression
(4) -> alt := altTypeOf(om,a,nil)$Lisp
(4) ()
Type: SExpression
(5) -> t1 := coerceInt(v,alt)$Lisp
(5) ()
Type: SExpression
(6) -> a := mkAtreeWithSrcPos(parseFromString("2")$Lisp,nil)$Lisp
(6) [--immediateData--,NIL,PositiveInteger()(),NIL,NIL]
Type: SExpression
(7) -> v := getValue(a)$Lisp
(7) ((PositiveInteger) . 2)
Type: SExpression
(8) -> om := objMode(v)$Lisp
(8) (PositiveInteger)
Type: SExpression
(9) -> alt := altTypeOf(om,a,nil)$Lisp
(9) (Integer)
Type: SExpression
(10) -> t1 := coerceInt(v,alt)$Lisp
(10) ((Integer) . 2)
Type: SExpression
(11) -> t1 := coerceOrRetract(t1,nil)$Lisp
(11) ()
Type: SExpression
(12) -> m := getMode(a)$Lisp
(12) ()
Type: SExpression
(13) -> o := objMode(v)$Lisp
(13) (PositiveInteger)
Type: SExpression
|
From vol5
|
All spad values in the interpreter are passed around in triples. These are lists of three items: [value,mode,environment]. The value may be wrapped (this is a pair whose CAR is the atom WRAPPED and whose CDR is the value), which indicates that it is a real value, or unwrapped in which case it needs to be EVALed to produce the proper value. The mode is the type of value, and should always be completely specified (not contain $EmptyMode). The environment is always empty, and is included for historical reasons. Modemaps:Modemaps are descriptions of compiled Spad function which the interpreter uses to perform type analysis. They consist of patterns of types for the arguments, and conditions the types must satisfy for the function to apply. For each function name there is a list of modemaps in file MODEMAP DATABASE for each distinct function with that name. The following is the list of the modemaps for "*" (multiplication. The first modemap (the one with the labels) is for module multiplication which is multiplication of an element of a module by a member of its scalar domain. This is the signature pattern for the modemap, it is of the form: (DomainOfComputation TargetType <ArgumentType ...>)
|
| This is the predicate that needs to be
| satisfied for the modemap to apply
| |
V |
/-----------/ |
( ( (*1 *1 *2 *1) V
/-----------------------------------------------------------/
( (AND (ofCategory *1 (Module *2)) (ofCategory *2 (SimpleRing))) )
. CATDEF) <-- This is the file where the function was defined
( (*1 *1 *2 *1)
( (AND (isDomain *2 (Integer)) (ofCategory *1 (AbelianGroup))) )
. CATDEF)
( (*1 *1 *2 *1)
( (AND
(isDomain *2 (NonNegativeInteger))
(ofCategory *1 (AbelianMonoid))) )
. CATDEF)
((*1 *1 *1 *1) ((ofCategory *1 (SemiGroup)) ) . CATDEF)
)
- |
Environments:
Environments associate properties with atoms.
(see CUTIL BOOT for the exact structure of environments).
Some common properties are:
modeSet:
During interpretation we build a modeSet property for each node in the expression. This is (in theory) a list of all the types possible for the node. In the current implementation these modeSets always contain a single type.
value:
Value properties are always triples. This is where the values of variables are stored. We also build value properties for internal nodes during the bottom up phase.
mode:
This is the declared type of an identifier.
Environments
There are several different environments used in the interpreter:
| $InteractiveFrame | This is the environment where the user values are stored. Any side effects of evaluation of a top-level expression are stored in this environment. It is always used as the starting environment for interpretation. |
| $e | This is the name used for $InteractiveFrame while interpreting. |
| $env | This is local environment used by the interpreter. Only temporary information (such as types of local variables is stored in $env. It is thrown away after evaluation of each expression. |
Type Inference
AST
From ptrees.boot:
Abstract Syntax Trees This file provides functions to create and examine abstract syntax trees. These are called pform, for short. The definition of valid pforms see ABSTRACT BOOT. !! This file also contains constructors for concrete syntax, although !! they should be somewhere else. THE PFORM DATA STRUCTURE Leaves: [hd, tok, pos] Trees: [hd, tree, tree, ...] hd is either an id or (id . alist) |
(1) -> pfExpression(a+b,1)$Lisp
(1) ((expression (posn . 1)) 1 b (1 0 . 1) (0 1 a (1 0 . 1)))
Type: SExpression
(3) -> pfLiteralString([a,b,c])$Lisp
(3) (2 3)
Type: SExpression
-- create an ID called a
(4) -> a:SExpression := pfId(a)$Lisp
(4) (id . a)
Type: SExpression
-- create an ID called b
(5) -> b:SExpression := pfId(b)$Lisp
(5) (id . b)
Type: SExpression
-- create and of a and b
(6) -> c:SExpression := pfAnd(a,b)$Lisp
(6) (And (id . a) (id . b))
Type: SExpression
-- display in in human readable form
(7) -> pfSexpr(c)$Lisp
(7) (And a b)
Type: SExpression
(8) ->
|
InputForm
This is defined in: mkfunc.spad.pamphlet
Any domain can control how it is parsed by defining:
convert(%) : InputForm
++ Domain of parsed forms which can be passed to the interpreter.
++ This is also the interface between algebra code and facilities
++ in the interpreter.
InputForm():
Join(SExpressionCategory(String, Symbol, Integer, DoubleFloat),
ConvertibleTo SExpression) with
interpret : % -> Any
++ interpret(f) passes f to the interpreter.
convert : SExpression -> %
++ convert(s) makes s into an input form.
binary : (%, List %) -> %
++ \spad{binary(op, [a1, ..., an])} returns the input form
++ corresponding to \spad{a1 op a2 op ... op an}.
function : (%, List Symbol, Symbol) -> %
++ \spad{function(code, [x1, ..., xn], f)} returns the input form
++ corresponding to \spad{f(x1, ..., xn) == code}.
lambda : (%, List Symbol) -> %
++ \spad{lambda(code, [x1, ..., xn])} returns the input form
++ corresponding to \spad{(x1, ..., xn) +-> code} if \spad{n > 1},
++ or to \spad{x1 +-> code} if \spad{n = 1}.
"+" : (%, %) -> %
++ \spad{a + b} returns the input form corresponding to \spad{a + b}.
"*" : (%, %) -> %
++ \spad{a * b} returns the input form corresponding to \spad{a * b}.
"/" : (%, %) -> %
++ \spad{a / b} returns the input form corresponding to \spad{a / b}.
"^" : (%, NonNegativeInteger) -> %
++ \spad{a ^ b} returns the input form corresponding to \spad{a ^ b}.
"^" : (%, Integer) -> %
++ \spad{a ^ b} returns the input form corresponding to \spad{a ^ b}.
0 : constant -> %
++ \spad{0} returns the input form corresponding to 0.
1 : constant -> %
++ \spad{1} returns the input form corresponding to 1.
flatten : % -> %
++ flatten(s) returns an input form corresponding to s with
++ all the nested operations flattened to triples using new
++ local variables.
++ If s is a piece of code, this speeds up
++ the compilation tremendously later on.
unparse : % -> String
++ unparse(f) returns a string s such that the parser
++ would transform s to f.
++ Error: if f is not the parsed form of a string.
parse : String -> %
++ parse(s) is the inverse of unparse. It parses a
++ string to InputForm
declare : List % -> Symbol
++ declare(t) returns a name f such that f has been
++ declared to the interpreter to be of type t, but has
++ not been assigned a value yet.
++ Note: t should be created as \spad{devaluate(T)$Lisp} where T is the
++ actual type of f (this hack is required for the case where
++ T is a mapping type).
compile : (Symbol, List %) -> Symbol
++ \spad{compile(f, [t1, ..., tn])} forces the interpreter to compile
++ the function f with signature \spad{(t1, ..., tn) -> ?}.
++ returns the symbol f if successful.
++ Error: if f was not defined beforehand in the interpreter,
++ or if the ti's are not valid types, or if the compiler fails. |