A scenegraph can be defined over various types of point and vectors:
- Cartesian Coordinates in 'n' dimensions.
- Complex Coordinates (Argand Plane).
- Conformal Coordinates in 'n' dimensions.
Each of these can be used with transforms, defined in various ways. On this page we will look at each type of space and see how it can be transformed.
There tends to be a natural matching between the coordinate type and the transform type as follows:
| Coordinates | transform type | alternative | other options |
|---|---|---|---|
| SCartesian(n) Cartesian |
matrix with (n+1)x(n+1) elements | function: Point ->Point | |
| SArgand Complex |
function: Complex DF -> Complex DF | function: Point ->Point | matrix |
| SConformal(n) Conformal |
multivector with 2(n+2) elements | function: Point ->Point | matrix |
However there are alternatives and we can often use different types and they will be converted by the code.
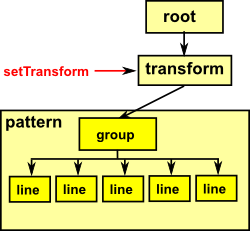 |
On this page we will use the graphics framework to experiment with transforms. In order that we can see the effect of the transform we will use a built in pattern (simple 'house' drawing), the reason for choosing this pattern is that it is not too complicated and it is asymmetrical so we can see the effect of reflections and so on. |
Here we will look at each type of space in turn as show how to apply transforms in that space which you can link to here:
- Transforms Using Cartesian Coordinates.
- Transforms in a Complex Plane.
- Transforms Using Conformal Coordinates.
Transforms Using Cartesian Coordinates.
The simplest way to transform Cartesian coordinates is to multiply by a matrix. So here we will use a transform node and set it with various matrix values. In this case we will work in 2 dimensions (in a plane) so we can define our scene over SCartesian(2). The dimension of the matrix should be one grater than this so we use a 3x3 matrix. The reason for this extra dimension is to use a projective space system which means we can translate in addition to rotating and scaling and so on.
First we create a simple shape as follows. In line (5) we include the transform node and set it to 'identity' to mean that, at this stage, it has no effect but we can change it later.
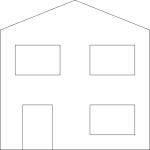 |
(1) -> DF ==> DoubleFloat
Type: Void
(2) -> PT ==> SCartesian(2)
Type: Void
(3) -> view := boxBoundary(sipnt(500,500)$PT,
sipnt(1200,1200)$PT)$SBoundary(PT)
(3) bound box:pt(500.0,500.0)->pt(1200.0,1200.0)
Type: SBoundary(SCartesian(2))
(4) -> sc := createSceneRoot(view)$Scene(PT)
(4) scene root bound box:pt(500.0,500.0)->pt(1200.0,1200.0) #ch=0
Type: Scene(SCartesian(2))
(5) -> tr := addSceneTransform(sc,identity()$STransform(PT))$Scene(PT)
(5) scene transform tr=iden #ch=0
Type: Scene(SCartesian(2))
(6) -> gd := addScenePattern(tr,"HOUSE"::Symbol,4,view)$Scene(PT)
(6)
scene line
[[pt(500.0,500.0),pt(500.0,535.0),....],
[pt(605.0,500.0),pt(640.0,500.0),....], ....]
#ch=0
Type: Scene(SCartesian(2))
(7) -> writeSvg(sc,"testGraph/example06a1.svg")
Type: Void |
We can then modify the the image by changing the transform in the existing transform node.
First we can try a simple translation. We will translate the 'house' right by 200 units and up by 200 units, so the put these values in the right hand column of the matrix. Apart from the translation, we don't want to change the shape in any other way, so the remainder of the matrix is an identity matrix. Note: the bottom right element of the matrix is set to 1, this is nearly always the case, if we were to set it to 0 then it would covert points to vectors which would not behave as expected of points in any subsequent transformations.
Here is the result of this below:
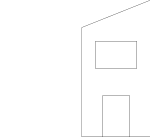 |
(8) -> offsetx := 200::DF
(8) 200.0
Type: DoubleFloat
(9) -> offsety := 200::DF
(9) 200.0
Type: DoubleFloat
(10) -> trb := stransform([[1::DF,0::DF,offsetx],_
[0::DF,1::DF,offsety],_
[0::DF,0::DF,1::DF]])$STransform(PT)
+1.0 0.0 200.0+
(10) mtx|0.0 1.0 200.0|
+0.0 0.0 1.0 +
Type: STransform(SCartesian(2))
(11) -> setTransform!(tr,trb)$Scene(PT)
Type: Void
(12) -> writeSvg(sc,"testGraph/example06b1.svg")
Type: Void |
Then we can apply a rotation, to rotate by the angle theta, about the origin, we use the following matrix:
| cos(theta) | sin(theta) |
| -sin(theta) | cos(theta) |
To make this into a 3x3 matrix we add a row below it consisting of zeroes and a column on the right containing the translation (in this case zero). Again the bottom right element of the matrix is set to 1, unless we want to convert the points to vectors, in which case we would set to zero..
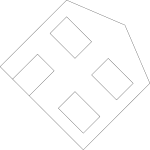 |
(13) -> theta:DF := (45::DF) * %pi /(180::DF)
(13) 0.7853981633974483
Type: DoubleFloat
(14) -> trc := stransform([[cos(theta),sin(theta),0::DF],_
[-sin(theta),cos(theta),0::DF],_
[0::DF,0::DF,1::DF]])$STransform(PT)
+0.7071067811865476 0.7071067811865475 0.0+
(14) mtx|-0.7071067811865475 0.7071067811865476 0.0|
+ 0.0 0.0 1.0+
Type: STransform(SCartesian(2))
(15) -> setTransform!(tr,trc)$Scene(PT)
Type: Void
(16) -> writeSvg(sc,"testGraph/example06c1.svg")
Type: Void |
Another type of transform is scaling. to do this we put the scale factor along the leading diagonal. Again the bottom right element is 1.
 |
(17) -> scale:DF := 0.25::DF
(17) 0.25
Type: DoubleFloat
(18) -> trd := stransform([[scale,0::DF,0::DF],_
[0::DF,scale,0::DF],_
[0::DF,0::DF,1::DF]])$STransform(PT)
+0.25 0.0 0.0+
(18) mtx|0.0 0.25 0.0|
+0.0 0.0 1.0+
Type: STransform(SCartesian(2))
(19) -> setTransform!(tr,trd)$Scene(PT)
Type: Void
(20) -> writeSvg(sc,"testGraph/example06d1.svg")
Type: Void |
There are many other types of transforms that we could apply, such as, reflection in a plane.
We can also combine transforms, such as those above, by either of the following which are equivalent to each other:
- Multiplying the matrices together.
- Nesting the transforms.
In both cases order is significant.
Transforms in a Complex Plane.
Transforms in a Complex Plane are done slightly differently than the above examples. In this case we need to supply the transform node with an appropriate function of the type:
Complex DF -> Complex DF.
This function implements typical transforms by a combination of the following:
| function | |
|---|---|
| translate | add complex number |
| rotate | multiply unit complex number |
| scale | multiply real |
First we create a simple shape as follows:
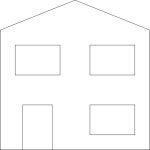 |
(1) -> DF ==> DoubleFloat
Type: Void
(2) -> C ==> Complex DF
Type: Void
(3) -> AR ==> SArgand
Type: Void
(4) -> view := boxBoundary(sipnt(500,500)$AR,sipnt(1200,1200)$AR)$SBoundary(AR)
(4) bound box:500.0 + %i500.0->1200.0 + %i1200.0
Type: SBoundary(SArgand)
(5) -> sc := createSceneRoot(view)$Scene(AR)
(5) scene root bound box:500.0 + %i500.0->1200.0 + %i1200.0 #ch=0
Type: Scene(SArgand)
(6) -> tr := addSceneTransform(sc,identity()$STransform(AR))$Scene(AR)
(6) scene transform tr=iden #ch=0
Type: Scene(SArgand)
(7) -> gd := addScenePattern(tr,"HOUSE"::Symbol,4,view)$Scene(AR)
(7)
scene line
[[500.0 + %i500.0,500.0 + %i535.0,....],
[605.0 + %i500.0,640.0 + %i500.0,....], ....]
#ch=0
Type: Scene(SArgand)
(8) -> writeSvg(sc,"testGraph/example06a2.svg")
Type: Void |
We can then modify the the image by changing the transform in the existing transform node.
First we can try a simple translation, this is done by creating a function which adds a constant complex number to its input.
 |
(9) -> translateComplex(x:C):C == x + complex(200::DF,200::DF)
Function declaration translateComplex : Complex(DoubleFloat) ->
Complex(DoubleFloat) has been added to workspace.
Type: Void
(10) -> trb := stransform(translateComplex)$STransform(AR)
Compiling function translateComplex with type Complex(DoubleFloat)
-> Complex(DoubleFloat)
(10) function as transform
Type: STransform(SArgand)
(11) -> setTransform!(tr,trb)$Scene(AR)
Type: Void
(12) -> writeSvg(sc,"testGraph/example06b2.svg")
Type: Void |
Then we can apply a rotation, this is done by creating a function which multiplies its input by a given complex number.
 |
(13) -> theta:DF := (45::DF) * %pi /(180::DF)
(13) 0.7853981633974483
Type: DoubleFloat
(14) -> rotateComplex(x:C):C == x * complex(cos(theta),sin(theta))
Function declaration rotateComplex : Complex(DoubleFloat) -> Complex
(DoubleFloat) has been added to workspace.
Type: Void
(15) -> trc := stransform(rotateComplex)$STransform(AR)
Compiling function rotateComplex with type Complex(DoubleFloat) ->
Complex(DoubleFloat)
(15) function as transform
Type: STransform(SArgand)
(16) -> setTransform!(tr,trc)$Scene(AR)
Type: Void
(17) -> writeSvg(sc,"testGraph/example06c2.svg")
Type: Void |
Scaleing, this is done by creating a function which scales its input by a DF value.
 |
(18) -> scale:DF := 0.25::DF
(18) 0.25
Type: DoubleFloat
(19) -> scaleComplex(x:C):C == x * scale
Function declaration scaleComplex : Complex(DoubleFloat) -> Complex(
DoubleFloat) has been added to workspace.
Type: Void
(20) -> trd := stransform(scaleComplex)$STransform(AR)
Compiling function scaleComplex with type Complex(DoubleFloat) ->
Complex(DoubleFloat)
(20) function as transform
Type: STransform(SArgand)
(21) -> setTransform!(tr,trd)$Scene(AR)
Type: Void
(22) -> writeSvg(sc,"testGraph/example06d2.svg")
Type: Void |
Transforms Using Conformal Coordinates.
First we create a simple shape as follows:
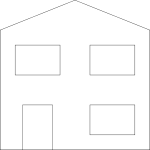 |
(1) -> DF ==> DoubleFloat
Type: Void
(2) -> CS ==> SConformal(2)
Type: Void
(3) -> view := boxBoundary(sipnt(500,500)$CS,
sipnt(1200,1200)$CS)$SBoundary(CS)
(3)
bound box:
(0.0, - 1.0, 250000.0, 0.0, 500.0, 0.0, 0.0, 0.0,
500.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
->
(0.0, - 1.0, 1440000.0, 0.0, 1200.0, 0.0, 0.0, 0.0,
1200.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
Type: SBoundary(SConformal(2))
(4) -> sc := createSceneRoot(view)$Scene(CS)
(4)
scene root
bound box:
(0.0, - 1.0, 250000.0, 0.0, 500.0, 0.0, 0.0, 0.0,
500.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
->
(0.0, - 1.0, 1440000.0, 0.0, 1200.0, 0.0, 0.0, 0.0,
1200.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
#ch=0
Type: Scene(SConformal(2))
(5) -> tr := addSceneTransform(sc,identity()$STransform(CS))$Scene(CS)
(5) scene transform tr=iden #ch=0
Type: Scene(SConformal(2))
(6) -> gd := addScenePattern(tr,"HOUSE"::Symbol,4,view)$Scene(CS)
(6)
scene line
[
[
(0.0, - 1.0, 250000.0, 0.0, 500.0, 0.0, 0.0, 0.0,
500.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
,
(0.0, - 1.0, 268112.5, 0.0, 500.0, 0.0, 0.0, 0.0,
535.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
,
....]
,
[
(0.0, - 1.0, 308012.5, 0.0, 605.0, 0.0, 0.0, 0.0,
500.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
,
(0.0, - 1.0, 329800.0, 0.0, 640.0, 0.0, 0.0, 0.0,
500.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0)
,
....]
,
....]
#ch=0
Type: Scene(SConformal(2))
(7) -> writeSvg(sc,"testGraph/example06a2.svg")
Type: Void
|
We can then modify the the image by changing the transform in the existing transform node.
First we can try a simple translation:
 |
(8) -> offsetx := 200::DF
(8) 200.0
Type: DoubleFloat
(9) -> offsety := 200::DF
(9) 200.0
Type: DoubleFloat
(10) -> trb := stransform([1::DF,0::DF,0::DF,0::DF,_
0::DF,0::DF,offsetx*(0.5::DF),0::DF,_
0::DF,0::DF,offsety*(0.5::DF),0::DF,_
0::DF,0::DF,0::DF,0::DF])$STransform(CS)
(10)
multiv[1.0,0.0,0.0,0.0,0.0,0.0,100.0,0.0,
0.0,0.0,100.0,0.0,0.0,0.0,0.0,0.0]
Type: STransform(SConformal(2))
(11) -> setTransform!(tr,trb)$Scene(CS)
Type: Void
(12) -> writeSvg(sc,"testGraph/example06b3.svg")
Type: Void |
Then we can apply a rotation:
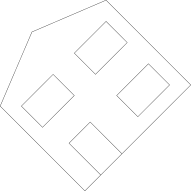 |
(13) -> theta:DF := (45::DF) * %pi /(180::DF)
(13) 0.7853981633974483
Type: DoubleFloat
(14) -> trc := stransform([cos(theta/2),0::DF,0::DF,0::DF,_
0::DF,0::DF,0::DF,0::DF,_
0::DF,0::DF,0::DF,0::DF,_
-sin(theta/2),0::DF,0::DF,0::DF])$STransform(CS)
(14)
multiv
[0.9238795325112867, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0,
0.0, 0.0, 0.0, 0.0, - 0.3826834323650898, 0.0, 0.0, 0.0]
Type: STransform(SConformal(2))
(15) -> setTransform!(tr,trc)$Scene(CS)
Type: Void
(16) -> writeSvg(sc,"testGraph/example06c3.svg")
Type: Void |
Scaleing:
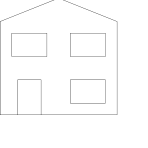 |
(17) -> scale:DF := 0.25::DF
(17) 0.25
Type: DoubleFloat
(18) -> trd := stransform(
[cosh(scale*0.5::DF),0::DF,0::DF,sinh(scale*0.5::DF),_
0::DF,0::DF,0::DF,0::DF,_
0::DF,0::DF,0::DF,0::DF,_
0::DF,0::DF,0::DF,0::DF])$STransform(CS)
(18)
multiv
[1.0078226778257109, 0.0, 0.0, 0.12532577524111546, 0.0,
0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
Type: STransform(SConformal(2))
(19) -> setTransform!(tr,trd)$Scene(CS)
Type: Void
(20) -> writeSvg(sc,"testGraph/example06d3.svg")
Type: Void
|
We can also do transform types that are not easy to do in other spaces such as reflection in unit circle:
(21) -> tre := stransform([0::DF,1::DF,-1000::DF,0::DF,_
0::DF,0::DF,0::DF,0::DF,_
0::DF,0::DF,0::DF,0::DF,_
0::DF,0::DF,0::DF,0::DF])$STransform(CS)
(21)
multiv[0.0,1.0,- 1000.0,0.0,0.0,0.0,0.0,0.0,
0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0]
Type: STransform(SConformal(2))
(22) -> setTransform!(tr,tre)$Scene(CS)
Type: Void
(23) -> writeSvg(sc,"testGraph/example06e3.svg")
Type: Void |
Comparison with legacy graphics framework
Existing transforms in Axiom (such as dhmatrix.spad.pamphlet and moebius.spad.pamphlet) are stand alone chunks of algebra which don't interwork with each other and it would be a lot of work to incorporate them into other code especially graphics and geometry.
The aim of STransform is to make a completely general template for transforms so that specific transforms like a Moebius transform could be implemented so that the slot directly into the geometry/graphics framework.
We have not achieved that aim yet. STransform does work with the various implementations of the SPointCategory such as SCartesian(2), SCartesian(3), SArgand and SConformal. What I would like to do is to have a transform category which could be implemented by domains like dhmatrix.spad.pamphlet and moebius.spad.pamphlet, then they could be used in the geometry/graphics framework anywhere transforms are appropriate.
The most general form of transform would be represented by PT->PT where PT is any implementation of SPointCategory. So ideally all transforms should be defined in this way. The usual way to transform a vector is to use a matrix like this:
transform(in:Vector,def:Matrix):Vector
So what I need is a way to curry it into something like this:
transform(def:Matrix):(Vector->Vector)
I don't know how to this? that is, how do I create an anonymous function where a variable (in this case def:Matrix) is a constant in the function?
Further Information
- User Reference on this page.
- Programmers Reference on this page.
- Examples of scenegraph structure on this page.
- The code is in file: scene.spad.pamphlet which is available from here.
- Existing Axiom graphics framework on this page.