BitStreams are potentially infinite in length. The elements of this domain are finite sequences that have not yet been completed. So we can think of these elements as approximations to the actual bitstream.
These BitStream representations are semidecidable, we can determine if two representations of streams are not equal but we cannot determine if they are equal. So if two streams are not unequal it does not follow that they are equal.
We cannot determine if they are equal because, however many terms of two streams that start with the same values we have, they might be still be extended with different values. We can never check the complete bitstream because we cannot hold an infinite structure in a finite computer.
| An example of a frame taken from Vickers section 3.7 |  |
| It may help to think of the structure as recursive? | 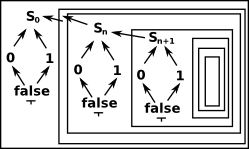 |
My initial code for this is on github here.
(1) -> a := starts("011")
(1) starts:011
Type: BitStreamFrame
(2) -> b := starts("001")
(2) starts:001
Type: BitStreamFrame
(3) -> a /\ b
(3) starts:011
starts:001
Type: BitStreamFrame
(4) ->
|
I think perhaps the code should be changed to have an explicit terminator (as in Winskel)? If the following streams are terminated, then we can say the following is true:
101 <= 101110
Where <= means 'is subset of', that is, it starts in the same way.
but if the streams are not terminated, we can only say maybe, not true.
101 <= 101110
because the streams may be extended to be different.