Since the graph structure contains optional layout information, then we need to have an algorithm for generating the layout information of the product from the layout information of its constituents. As requested by Ralf I have documented the algorithm that I used on this page.
Calculating the position of vertices for tensor and Cartesian products.
This is a very simple algorithm and it does not attempt to adjust the position of the vertices so that edges don't cross intermediate vertices and so on. It would be nice to have a more sophisticated algorithm but I'm not sure this is really core functionality for a CAS?
Both tensor and Cartesian products produce the same number of verities (the difference between tensor and Cartesian products is in the edges) and so I have used the same algorithm to generate the coordinates of both types of product.
If the number of points in graph A is #a,
and the number of points in graph B is #b,
then the number of points in their product P is: #a * #b.
The position of each of these points is given by:
x:NNI := bxi*diagramWidth(A)+axi y:NNI := byi*diagramHeight(A)+ayi
Where
- x = x coordinate of vertex in product.
- y = y coordinate of vertex in product.
- axi,bxi = x coordinate of vertex in a or b.
- ayi,byi = y coordinate of vertex in a or b.
Note: NNI is used instead of float to keep the SVG small since it is good enough to place the points on a relatively course lattice.
Possible VariationThis does not quite fit into a 2 dimensional vector equation because the scale factor is different in each dimension, but if we wanted to scale the same in both dimensions we could use a 2D vector equation: pointP := pointB * scaleFactor + pointA where: scaleFactor := max(diagramWidth(a),diagramHeight(a)) |
Example
| A | 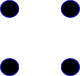 |
| B | 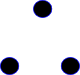 |
| A*B | 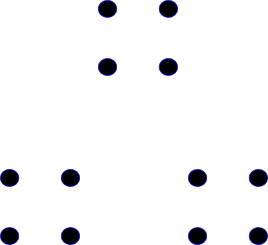 |
| B*A | 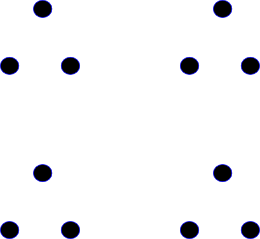 |
Calculating the position of vertices for sum and merge
This is much simpler, we just have to offset one of the graphs so that they do not overlap.
That is, the vertices from A use the coordinates that they already have and the vertices from B have a fixed offset added to their coordinates (for example add diagramWidth(a) to their x coordinate).