This is a continuation of the tutorial for the graph theory code which starts here. If you have not already installed and loaded the code from 'graph.spad' then you first need to follow the instructions on that page.
On this page we look at specialised variants of graph:
Function Graphs
FunctionGraph is similar to DirectedGraph except there is only one arrow out of each vertex.
In order to work with adjoint mappings we need to work with function graphs, this is like directional graph except that each vertex has exactly one outgoing arrow. We can construct FunctionGraph in varous ways (the tutorial on this page has more information). Here we construct a function graph using the same structures that we used for DirectedGraph:
(1) -> FG := FunctionGraph(String)
(1) FunctionGraph(String)
Type: Type
(2) -> OBJT ==> Record(value:String,posX:NNI,posY:NNI)
Type: Void
(3) -> oba:OBJT := ["a",2,2]
(3) [value= "a",posX= 2,posY= 2]
Type: Record(value:
String,posX: NonNegativeInteger,posY: NonNegativeInteger)
(4) -> obb:OBJT := ["b",2,4]
(4) [value= "b",posX= 2,posY= 4]
Type: Record(value:
String,posX: NonNegativeInteger,posY: NonNegativeInteger)
(5) -> ara:ARRW := ["alpha",0,1,2,0,0]
(5) ["alpha",0,1,2,0,0]
Type: List(Any)
(6) -> arb:ARRW := ["beta",0,2,1,0,0]
(6) ["beta",0,2,1,0,0]
Type: List(Any)
(7) -> fs1 := functionGraph([oba,obb],[ara,arb])$FG
(7) "a,b|1:a->b,2:b->a"
Type: FunctionGraph(String)
|
Tensor product of Function Graphs
Not all the functions that apply to DirectedGraph can be applied to FunctionGraph. Below we construct a Tensor product of two graphs, however we cannot construct a Cartesian product of two function graphs because that would require two arrows per vertex.
(8) -> hs1 := cycleClosed(["a","b","c"],"a")$FG
(8) "a,b,c|1:a->b,2:b->c,3:c->a"
Type: FunctionGraph(String)
(9) -> hs2 := cycleOpen(["1","2","3"],"b")$FG
(9) "1,2,3|1:1->2,2:2->3,3:3->3"
Type: FunctionGraph(String)
(10) -> hs3 := closedTensor(hs1,hs2,concat)$FG
(10)
"a1,a2,a3,b1,b2,b3,c1,c2,c3|1:a1->b2,2:a2->b3,3:a3->b3,
4:b1->c2,5:b2->c3,6:b3->c3,7:c1->a2,8:c2->a3,9:c3->a3"
Type: FunctionGraph(String)
(11) -> diagramSvg("testGraph7s1.svg",hs3,true)
Type: Void |
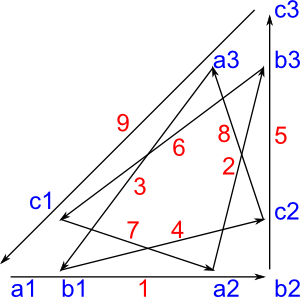 |
I have modified the diagram on the left by hand (using Inkscape) to seperate out the arrows a bit and to colour the vertex and arrow names. |
Apply to Function Graphs
Apply takes a vertex and returns the next vertex. Since, in a function graph, there is only one outgoing arror this is always a single vertex.
(12) -> a := apply(hs3,1::NNI)
(12) 5
Type: PositiveInteger
(13) -> a := apply(hs3,a)
(13) 9
Type: PositiveInteger
(14) -> a := apply(hs3,a)
(14) 3
Type: PositiveInteger
|
Limit of Function Graphs
In a finite function graph, if we keep applying the function, then we must eventually reach a loop since we will eventually run out of new verticies to visit. 'limit' returns this loop for a given starting point.
(15) -> limit(hs3,1::NNI)
(15) "[->3->6->9]"
Type: Loop
|
Map of Function Graphs
We can now map this graph to create another graph as follows:
(16) -> hs4 := map(hs3,[1::NNI,1::NNI,1::NNI,_
2::NNI,2::NNI,2::NNI,_
3::NNI,3::NNI,3::NNI],["x","y","z"],0,0)
(16) "x,y,z|1:x->y,2:y->z,3:z->x"
Type: FunctionGraph(String)
(17) -> diagramSvg("testGraph7s2.svg",hs4,true)
Type: Void |
 |
Again, I have modifie the diagram using Inkscape |
'coAdjoint' returns an inverse mapping to the one given. Where the composed mappings produce a graph where the arrows go in the same direction as the original graph.
(18) -> coAdjoint(hs3,[1::NNI,1::NNI,1::NNI,_
2::NNI,2::NNI,2::NNI,_
3::NNI,3::NNI,3::NNI])
(18) [3,6,9]
Type: Union(List(NonNegativeInteger),...)
|
'contraAdjoint' returns an inverse mapping to the one given. Where the composed mappings produce a graph where the arrows go in the opposite direction as the original graph.
(19) -> contraAdjoint(hs3,[1::NNI,1::NNI,1::NNI,_
2::NNI,2::NNI,2::NNI,_
3::NNI,3::NNI,3::NNI])
(19) "failed"
Type: Union("failed",...) |
Undirected Graphs
In an undirected graph an arrow a->b is also considered to be b->a, that is, arrows are double ended (or do not have direction).
In the example below we create a graph with arrows that, in other types of graph, would be unidirectional arrows, however in 'UndirectedGraph' they are treated as bidirectional arrows. In the example below we can see that the distanceMatrix is symmetrical about the leading diagonal.
(20) -> UG := UndirectedGraph(String)
(20) UndirectedGraph(String)
Type: Type
(21) -> us1 := cycleClosed(["a","b","c"],"a")$UG
(21) "a,b,c|a1:a->b,a2:b->c,a3:c->a,a1:b->a,a2:c->b,a3:a->c"
Type: UndirectedGraph(String)
(22) -> distanceMatrix(us1)
+0 1 1+
(22) |1 0 1|
+1 1 0+
Type: Matrix(Integer)
|
Multifunction Graphs
In a multifunction graph each vertex has the same number of outgoing arrows. So a MultifunctionGraph is similar to a FunctionGraph except that, instead of each vertex having one outgoing arrow, in this case it will have 'n' outgoing arrows (where 'n' is the same for all vertices in the graph).
(23) -> MG := MultifunctionGraph(String)
(23) MultifunctionGraph(String)
Type: Type
(24) -> MFOBJT ==> Record(value:String,posX:NNI,posY:NNI,next:List NNI)
Type: Void
(25) -> moba:MFOBJT := ["a",2,2,[2,3]]
(25) [value= "a",posX= 2,posY= 2,next= [2,3]]
Type: Record(value: String,posX: NonNegativeInteger,
posY: NonNegativeInteger,next: List(NonNegativeInteger))
(26) -> mobb:MFOBJT := ["b",2,4,[3,1]]
(26) [value= "b",posX= 2,posY= 4,next= [3,1]]
Type: Record(value: String,posX: NonNegativeInteger,
posY: NonNegativeInteger,next: List(NonNegativeInteger))
(27) -> mobc:MFOBJT := ["b",4,4,[1,2]]
(27) [value= "b",posX= 4,posY= 4,next= [1,2]]
Type: Record(value: String,posX: NonNegativeInteger,
posY: NonNegativeInteger,next: List(NonNegativeInteger))
(28) -> mf1 := multifunctionGraph([moba,mobb,mobc])$MG
(28) "a,b,b|1:a->b,2:b->b,3:b->a"
Type: MultifunctionGraph(String)
(29) -> b := apply(mf1,1::NNI,1::NNI)
(29) 2
Type: PositiveInteger
(39) -> b := apply(mf1,b,1::NNI)
(30) 3
Type: PositiveInteger
(39) -> b := apply(mf1,b,1::NNI)
(31) 1
Type: PositiveInteger
(39) -> c := apply(mf1,1::NNI,2::NNI)
(32) 3
Type: PositiveInteger
(39) -> c := apply(mf1,c,2::NNI)
(33) 2
Type: PositiveInteger
(39) -> c := apply(mf1,c,2::NNI)
(34) 1
Type: PositiveInteger
|
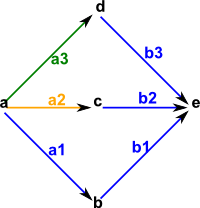
Weighted Graphs
This graph assigns a weight to each arrow. This is used when calculating routes.
So far route will find the route between two given nodes with the minimum number of hops. However we may want to choose some other metric to minimise when choosing a route. 'WeightedGraph' is a specialised Graph which has an OrderedAbelianMonoid value for each vertex and each arrow (although currently only the arrow values are used).
This graph assigns a weight to each arrow. This is used when calculating say, lowest 'cost' routes.
An arrow with a higher weight is more 'costly' in some way and therefore we try to choose the minimum weight.
- For arrows in series the overall weight is the sum of the individual weights.
- For arrows in parallel the overall weight is the minimum of the individual weights.
I may change this in future to allow different cost metrics to be plugged in.
(18) -> WG := WeightedGraph(String,NNI)
(18) WeightedGraph(String,NonNegativeInteger)
Type: Type
(19) -> WOBJT ==> Record(value:String,posX:NNI,posY:NNI,weight:NNI)
Type: Void
(20) -> oba:WOBJT := ["a",10,30,1::NNI]
(20) [value= "a",posX= 10,posY= 30,weight= 1]
Type: Record(value: String,posX: NonNegativeInteger,_
posY: NonNegativeInteger,weight: NonNegativeInteger)
(21) -> obb:WOBJT := ["b",30,10,2::NNI]
(21) [value= "b",posX= 30,posY= 10,weight= 2]
Type: Record(value: String,posX: NonNegativeInteger,_
posY: NonNegativeInteger,weight: NonNegativeInteger)
(22) -> obc:WOBJT := ["c",30,30,3::NNI]
(22) [value= "c",posX= 30,posY= 30,weight= 3]
Type: Record(value: String,posX: NonNegativeInteger,_
posY: NonNegativeInteger,weight: NonNegativeInteger)
(23) -> obd:WOBJT := ["d",30,50,4::NNI]
(23) [value= "d",posX= 30,posY= 50,weight= 4]
Type: Record(value: String,posX: NonNegativeInteger,_
posY: NonNegativeInteger,weight: NonNegativeInteger)
(24) -> obe:WOBJT := ["e",50,30,5::NNI]
(24) [value= "e",posX= 50,posY= 30,weight= 5]
Type: Record(value: String,posX: NonNegativeInteger,_
posY: NonNegativeInteger,weight: NonNegativeInteger)
(25) -> hs4 := weightedGraph([oba,obb,obc,obd,obe])$WG
(25) "a,b,c,d,e"
Type: WeightedGraph(String,NonNegativeInteger)
(26) -> addWArrow!(hs4,"a1",1,2,1)$WG
(26) "a,b,c,d,e|a1:a->b"
Type: WeightedGraph(String,NonNegativeInteger)
(27) -> addWArrow!(hs4,"a2",1,3,4)$WG
(27) "a,b,c,d,e|a1:a->b,a2:a->c"
Type: WeightedGraph(String,NonNegativeInteger)
(28) -> addWArrow!(hs4,"a3",1,4,9)$WG
(28) "a,b,c,d,e|a1:a->b,a2:a->c,a3:a->d"
Type: WeightedGraph(String,NonNegativeInteger)
(29) -> addWArrow!(hs4,"b1",2,5,9)$WG
(29) "a,b,c,d,e|a1:a->b,a2:a->c,a3:a->d,b1:b->e"
Type: WeightedGraph(String,NonNegativeInteger)
(30) -> addWArrow!(hs4,"b2",3,5,4)$WG
(30) "a,b,c,d,e|a1:a->b,a2:a->c,a3:a->d,b1:b->e,b2:c->e"
Type: WeightedGraph(String,NonNegativeInteger)
(31) -> addWArrow!(hs4,"b3",4,5,1)$WG
(31) "a,b,c,d,e|a1:a->b,a2:a->c,a3:a->d,b1:b->e,b2:c->e,b3:d->e"
Type: WeightedGraph(String,NonNegativeInteger)
(32) -> diagramSvg("testGraph6s2.svg",hs4,true)
Type: Void
(33) -> weightedDistanceMatrix(hs4)
(33)
[0, 1, 4, 9, 8,_
disjoint, 0, disjoint, disjoint, 9,_
disjoint, disjoint, 0, disjoint, 4,_
disjoint, disjoint, disjoint, 0, 1,_
disjoint, disjoint, disjoint, disjoint, 0]
Type: TwoDimensionalArray(Union(NonNegativeInteger,disjoint)) |