This is a continuation of the tutorial for the graph theory code which starts here. If you have not already installed and loaded the code from 'graph.spad' then you first need to follow the instructions on that page.
On this page we explore the complement of a graph.
The complement or inverse of a graph is a graph on the same vertices such that there is an arrow if and only if there is not an arrow in its complement. That is, it is the complement of the arrows but is not the set complement. for more information see this wiki page.
(1) -> GS := DirectedGraph(String)
(1) DirectedGraph(String)
Type: Type
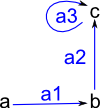
(2) -> hs1 := cycleOpen(["a","b","c"],"a")$GS
(2) "a,b,c|a1:a->b,a2:b->c,a3:c->c"
Type: DirectedGraph(String)
(3) -> diagramSvg("testGraph5c1.svg",hs1,true)
Type: Void |
First lets create some operands:
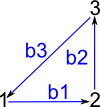
(4) -> hs2 := cycleClosed(["1","2","3"],"b")$GS
(4) "1,2,3|b1:1->2,b2:2->3,b3:3->1"
Type: DirectedGraph(String)
(5) -> diagramSvg("testGraph5c2.svg",hs2,true)
Type: Void |
and another:
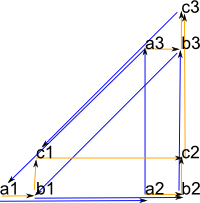
(6) -> hs3 := closedTensor(hs1,hs2,concat)$GS
(6)
"a1,a2,a3,b1,b2,b3,c1,c2,c3|a1*b1:a1->b2,a1*b2:a2->b3,
a1*b3:a3->b1,a2*b1:b1->c2,a2*b2:b2->c3,a2*b3:b3->c1,
a3*b1:c1->c2,a3*b2:c2->c3,a3*b3:c3->c1"
Type: DirectedGraph(String)
(7) -> adjacencyMatrix(hs3)
+0 0 0 0 0 0 0 0 0+
|0 0 0 0 0 0 0 0 0|
|0 0 0 0 0 0 0 0 0|
|0 0 1 0 0 0 0 0 0|
(7) |1 0 0 0 0 0 0 0 0|
|0 1 0 0 0 0 0 0 0|
|0 0 0 0 0 1 0 0 1|
|0 0 0 1 0 0 1 0 0|
+0 0 0 0 1 0 0 1 0+
Type: Matrix(NonNegativeInteger)
(8) -> diagramSvg("testGraph5c3.svg",hs3,true)
Type: Void |
Then, for reference, this is what a tensor looks like

(9) -> hs4 := closedCartesian(hs1,hs2,concat)$GS
(9)
"a1,a2,a3,b1,b2,b3,c1,c2,c3|b1#1:a1->a2,b2#1:a2->a3,b3#1:a3->a1,
a1#1:a1->b1,a1#2:a2->b2,a1#3:a3->b3,b1#2:b1->b2,b2#2:b2->b3,
b3#2:b3->b1,a2#1:b1->c1,a2#2:b2->c2,a2#3:b3->c3,a3#1:c1->c1,
b1#3:c1->c2,a3#2:c2->c2,b2#3:c2->c3,b3#3:c3->c1,a3#3:c3->c3"
Type: DirectedGraph(String)
(10) -> adjacencyMatrix(hs4)
+0 0 1 0 0 0 0 0 0+
|1 0 0 0 0 0 0 0 0|
|0 1 0 0 0 0 0 0 0|
|1 0 0 0 0 1 0 0 0|
(10) |0 1 0 1 0 0 0 0 0|
|0 0 1 0 1 0 0 0 0|
|0 0 0 1 0 0 1 0 1|
|0 0 0 0 1 0 1 1 0|
+0 0 0 0 0 1 0 1 1+
Type: Matrix(NonNegativeInteger)
(11) -> diagramSvg("testGraph5c4.svg",hs4,false)
Type: Void |
and this is cartesian product
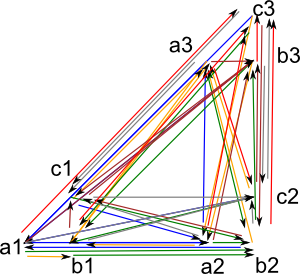
(12) -> hs5 := ~ closedTensor(~hs1,~hs2,concat)$GS
(12)
"a1,a2,a3,b1,b2,b3,c1,c2,c3|12:a1->a2,14:a1->b1,15:a1->b2,
16:a1->b3,18:a1->c2,23:a2->a3,24:a2->b1,25:a2->b2,26:a2->b3,
29:a2->c3,31:a3->a1,34:a3->b1,35:a3->b2,36:a3->b3,37:a3->c1,
42:b1->a2,45:b1->b2,47:b1->c1,48:b1->c2,49:b1->c3,53:b2->a3,
56:b2->b3,57:b2->c1,58:b2->c2,59:b2->c3,61:b3->a1,64:b3->b1,
67:b3->c1,68:b3->c2,69:b3->c3,72:c1->a2,75:c1->b2,77:c1->c1,
78:c1->c2,79:c1->c3,83:c2->a3,86:c2->b3,87:c2->c1,88:c2->c2,
89:c2->c3,91:c3->a1,94:c3->b1,97:c3->c1,98:c3->c2,99:c3->c3"
Type: DirectedGraph(String)
(13) -> adjacencyMatrix(hs5)
+0 0 1 0 0 1 0 0 1+
|1 0 0 1 0 0 1 0 0|
|0 1 0 0 1 0 0 1 0|
|1 1 1 0 0 1 0 0 1|
(13) |1 1 1 1 0 0 1 0 0|
|1 1 1 0 1 0 0 1 0|
|0 0 1 1 1 1 1 1 1|
|1 0 0 1 1 1 1 1 1|
+0 1 0 1 1 1 1 1 1+
Type: Matrix(NonNegativeInteger)
(14) -> diagramSvg("testGraph5c5.svg",hs5,false)
Type: Void |
So here is the complement of the tensor poduct of the two complements:
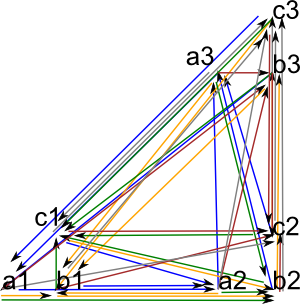
(15) -> hs6 := ~ closedCartesian(~hs1,~hs2,concat)$GS
(15)
"a1,a2,a3,b1,b2,b3,c1,c2,c3|12:a1->a2,14:a1->b1,15:a1->b2,16:a1->b3,
18:a1->c2,19:a1->c3,23:a2->a3,24:a2->b1,25:a2->b2,26:a2->b3,27:a2->c1,
29:a2->c3,31:a3->a1,34:a3->b1,35:a3->b2,36:a3->b3,37:a3->c1,38:a3->c2,
42:b1->a2,43:b1->a3,45:b1->b2,47:b1->c1,48:b1->c2,49:b1->c3,51:b2->a1,
53:b2->a3,56:b2->b3,57:b2->c1,58:b2->c2,59:b2->c3,61:b3->a1,62:b3->a2,
64:b3->b1,67:b3->c1,68:b3->c2,69:b3->c3,72:c1->a2,73:c1->a3,75:c1->b2,
76:c1->b3,78:c1->c2,81:c2->a1,83:c2->a3,84:c2->b1,86:c2->b3,89:c2->c3,
91:c3->a1,92:c3->a2,94:c3->b1,95:c3->b2,97:c3->c1"
Type: DirectedGraph(String)
(16) -> adjacencyMatrix(hs6)
+0 0 1 0 1 1 0 1 1+
|1 0 0 1 0 1 1 0 1|
|0 1 0 1 1 0 1 1 0|
|1 1 1 0 0 1 0 1 1|
(16) |1 1 1 1 0 0 1 0 1|
|1 1 1 0 1 0 1 1 0|
|0 1 1 1 1 1 0 0 1|
|1 0 1 1 1 1 1 0 0|
+1 1 0 1 1 1 0 1 0+
Type: Matrix(NonNegativeInteger)
(17) -> diagramSvg("testGraph5c6.svg",hs6,false)
Type: Void |
and here is the complement of the cartesian poduct of the two complements: