Concurrent, Coplanar Forces
Concurrent, coplanar forces are forces which act through one point and are in one plane.
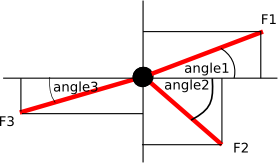
Triangle Of Forces
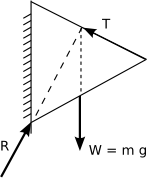
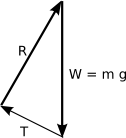
For three co-planar forces to be in equilibrium they must be concurrent. A triangle of forces can then represent the forces in magnitude and direction.
Jib Crane |
Triangle of Forces |
Polygon Of Forces
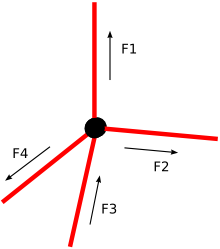
If more than three forces act on a body they may be represented in magnitude and direction by the sides of a polygon:
Forces at a joint |
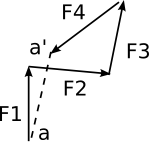
Polygon of forces |
If a closed polygon results, then the forces are in equilibrium. If an open polygon results, then aa' is the resultant (opposes flow of arrows) aa' is known as the equilibrant (follows flow of arrows).
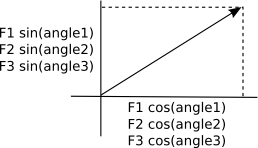
Resolution of Forces
Any single force can be replaced by two others at right angles to each other, known as horizontal and vertical components.
|
|
Example
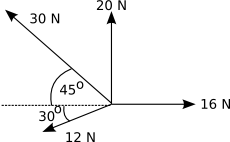
The following forces act at a point:
- 16 newtons due east
- 20 newtons due north
- 30 newtons north west
- 12 newtons 30° south of west
Determine the magnitude and direction of the resultant of these forces when they are pulling away from the point
a) by drawing the polygon of forces
b) by resolving the forces
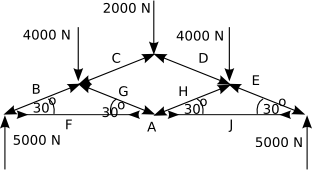
Frameworks
For frameworks we can combine the polygon of forces for each joint in the framework to give a combined force diagram.
For each instance of a framework we can draw two complimentary diagrams:
- A Space Diagram - shows the actual physical construction of the framework.
- A Force diagram - shows the combined polygon of forces.
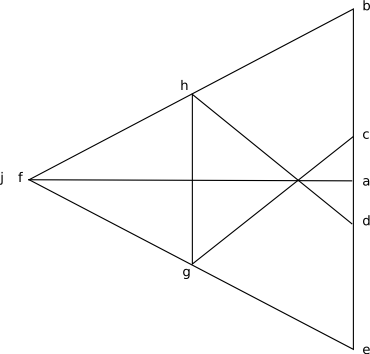
In the space diagram we can denote struts and ties as follows:
![]()
The two diagrams are complementary, the lines in the space diagram correspond to the points in the force diagram and the points in the space diagram correspond to the lines in the force diagram. The lines (struts or ties) in the space diagram are marked by upper case letters, there are corresponding lower case letters shown for the points in the force diagram.