Imagine a force acting on node B as follows:
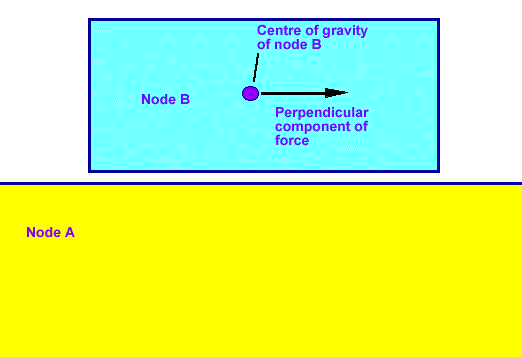
Then node B will accelerate with a value of Fb/mb as given by newtons law.
What happens if we now add another force normal to the surfaces tending to push the nodes together (assume node A is fixed and there is an equal and opposite reaction normal to the surface). What effect will this have on the perpendicular acceleration?
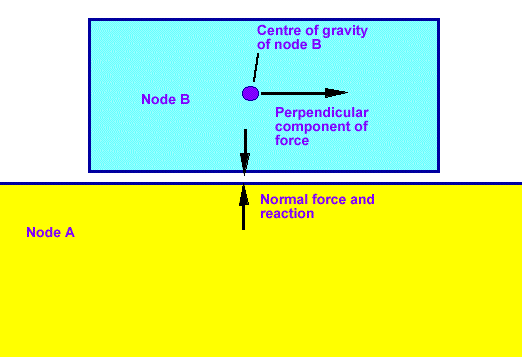
This contact between the two objects will cause the perpendicular motion to slow down because of the friction caused by small irregularities in the surfaces.
But how do we quantify this friction force?
The coefficient of friction is defined as the ratio of the magnitude of the frictional force and the normal force:
u = fk / fn
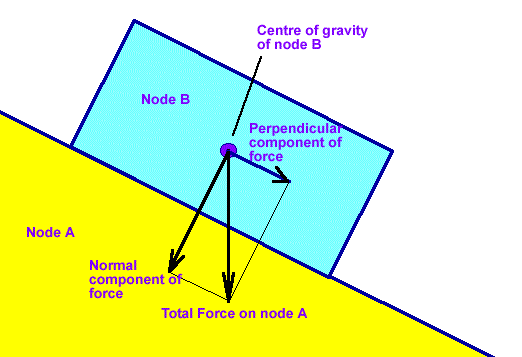
Assuming the other parameters don't cause them to bounce off then, their relative motion will be determined by the coefficient of friction of each node and the Normal and Perpendicular components of the force.




