On the last page we derived some rotation concepts applied to an infinitesimally small particle. Here we calculate these concepts for solid objects by integrating the equations for a particle across the whole object.
Angular Velocity (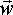 )
)
As seen in the Angular Velocity of particle section, angular velocity depends on the point that we are measuring the rotation about. So for a solid object, the angular velocity of all the particles, from which it is composed, are different.
Only when we are measuring the rotation about the centre of rotation is the rotation of all points on the object the same. So, for that reason, when we are talking about the angular velocity of a solid object we mean the angular velocity about its centre of rotation.
If an object is moving in free space, with no external forces or torques acting on it, then it will rotate about its centre-of-mass. So we can represent the total instantaneous motion of a rigid body by a combination of the linear velocity of its centre of mass and its rotation about its centre of mass.
In the pages about kinematics the position of an unconstrained rigid body was represented by 6 dimensional vector as follows:
| wx | angular velocity the about x axis (radians per second) |
| wy | angular velocity the about x axis (radians per second) |
| wz | angular velocity the about x axis (radians per second) |
| vx | linear velocity of centre of mass along x axis (metres per second) |
| vy | linear velocity of centre of mass along y axis (metres per second) |
| vz | linear velocity of centre of mass along z axis (metres per second) |
Further information about angular velocity.
Angular Momentum (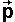 )
)
As we saw here, the instantaneous angular momentum of a particle, about a given point) is the product of its mass and its angular velocity.
For a solid object, its angular momentum about a given point, is the integral of the instantaneous angular momentums of all the particles across the volume
![]() ==
==![]()
![]()
![]() (
(
![]() x
x ![]() )dm
)dm
| where: | |||
symbol |
description |
type |
units |
| the instantaneous angular momentum about PC | bivector | kg m2/s | |
| x | the cross product operator(see here for definition) | ||
| the instantaneous position of
the particle relative to point |
vector | m | |
| the instantaneous linear momentum
of the particle = m |
vector | kg m/s | |
| dm | the mass of the particle. | scalar | kg |
As with angular velocity, the angular momentum of a point is not an absolute value, but it depends on which point that the rotation is measured about. However, since Angular Momentums can be added (provided they are about the same point) then it is possible to give the angular momentum of a rigid body about any point.
As discussed here, angular momentum of any closed system is conserved.
So for a rigid body, rotating about its centre of mass, then the angular momentum of the whole system (about any point) is conserved.
If a system has objects which have linear velocity, along a line offset from
the point about which the momentum is measured, then this will contribute to
the systems angular momentum, event if the object is not rotating. This is because
the cross product ![]() x
x ![]() is not zero.
is not zero.
The angular momentum about any point ![]() is the angular momentum about the centre of mass, plus the angular momentum
associated with the motion of the centre of mass about
is the angular momentum about the centre of mass, plus the angular momentum
associated with the motion of the centre of mass about ![]() .
.
The instantaneous position and the instantaneous momentum will defines the status of a solid object. If we also know constants for the object such as its shape and inertia tensor matrix, and we know all the forces acting on the object, then we can predict its future states.
| θx | angle about x |
| θy | angle about y |
| θz | angle about z |
| Px | position of centre of mass along x axis |
| Py | position of centre of mass along y axis |
| Pz | position of centre of mass along z axis |
| lx | angular momentum about x |
| ly | angular momentum about y |
| lz | angular momentum about z |
| mvx | momentum along x axis |
| mvy | momentum along y axis |
| mvz | momentum along z axis |
Angular Acceleration (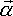 )
)
As seen in the Angular Acceleration of particle section, angular acceleration depends on the point that we are measuring the rotation about. So for a solid object, the angular acceleration of all the particles, from which it is composed, are different.
As for angular rotation, the angular acceleration, about the centre of rotation,
for all points on the object will be the same. So, for that reason, when we
are talking about the angular acceleration of a solid object we mean the angular
acceleration about its centre of rotation. This will be the rate of change of
angular velocity ![]() =d
=d![]() / dt. When measured from the centre of rotation the centrifugal angular acceleration
is zero.
/ dt. When measured from the centre of rotation the centrifugal angular acceleration
is zero.
We can represent the total instantaneous acceleration of a rigid body by a combination of the linear acceleration of its centre of mass and its acceleration about its centre of mass.
Torque (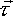 )
)
A torque is a turning force. It is applied to a rigid object, by two equal and opposite forces, which are offset.
The total torque about a point is the force times its perpendicular distance from the centre of rotation, summed for all points
If we apply a force to a free floating solid body then, there is an equal and opposite force acting on the centre of mass of the object. If these forces are offset then a torque exists. So a single applied force can produce both, a linear and rotational movement.
So, if a system of forces are applied to a solid object then, they can be replaced by an equivalent linear force on the centre of mass plus, a torque about the centre of mass.
Inertia [I]
As we saw here that, for a particle:
|
So integrate these across a solid volume gives:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
These terms are calculated in the frame of reference of the object itself. If the object is rotating and if we want to work in an absolute frame-of-reference then, we need to translate these terms to the absolute frame-of-reference. This will then mean that these terms are varying with time (in the frame of reference of the object they are constant).
So the equations for rotation are a lot more complicated than linier motion because torque in one dimention can cause angular acceleration in another dimention. However, it turns out that is always possible to choose a local coordinate system where the inertia matrix is diagonal:
|
The oreintation of this coordinate system can be found by using the eigen vectors. There are examples of this under table-top-physics under, twomasses twomasses45degrees, and threemasses.
So should we assume that all VRML shapes are defined in a local coordinate system where this is true? well Box, Sphere, Cylinder and Cone will be, but I dont thing that we can assume that IFS, Extrude, ElivationGrid are. We could make sure that we define the points in the IFS so that it is, but I am not sure that we can impose that restriction.


