On this page we will just be considering linear motion, other pages will then go on to consider the more general case which includes rotation.
For there to be no rotational motion, we could either assume that the object being considered is a particle (its mass is concentrated on a single point). or we could assume that any forces acting on the object are acting on its centre-of-mass.
Newtons Laws
Newtons laws are normally stated in some form like the following.
- First Law - An object at rest stays at rest unless acted on by an external force. An object in motion continues to travel with constant velocity unless acted on by an external force.
- Second Law - The acceleration of an object is in the direction of the net external force acting on it. It is proportional to the net external force, and is inversely proportional to the mass of the object.
- Third Law - Forces always occur in equal and opposite pairs. If object A exerts a force on object B, an equal but opposite force is exerted by object B on object A.
These laws are defined for linear motion as opposed to rotational motion. Euler defined similar laws for rotating objects, but before we go on to work out general laws for an object with both linear and angular motion, I think it is is important to be very clear about our assumptions.
So on this page we will just be considering linear motion. For there to be no rotational motion, we could either assume that the object being considered is a particle (its mass is concentrated on a single point). or we could assume that any forces acting on the object are acting on its centre-of-mass.
The relationship between force and acceleration is quantified by Newtons second law which says that the acceleration is:
- Proportional to the net external force.
- Inversely proportional to its mass.
- In the direction of the force.
So if we choose the units correctly, then:
F=ma
| where: | |||
symbol |
description |
type |
units |
| F | net force | vector | kg m/s2 |
| m | mass | scalar | kg |
| a | acceleration | vector | m/s2 |
An alternative form of this equation is that Force is the rate of change of momentum, or integrating both sides gives: momentum is the line integral of force.
I think it is important to be very clear about assumptions and conditions involved with this equation. This may seem pedantic, but when we go on to the case where the object is rotating, then things get more complicated and less initiative. So the rest of this page is to make sure our understanding is as clear as possible.
Inertia and external forces
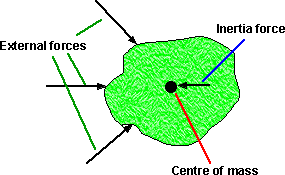
The F in the above equation is the net external force, in other words the vector sum of all the external forces. This external force is matched by an equal and opposite 'internal' or 'inertia' force (as expected from the third law). This inertia force can be thought of as the resistance of mass to chance of velocity. Of coarse this inertia force should not be included in the F=ma equation (otherwise the resultant force would always be zero) but it is a 'real' force, for instance, it will have an effect on other objects and it may be involved when we consider rotations. For example try accelerating a large mass (not against gravity) and you can feel the inertia force reacting against the acceleration.
Vector form of equation
So far we are measuring the force and acceleration along the direction that they are acting. When we are doing this we can work in one dimension and use scalars for all quantities.
When we are simulating physics in our program we may be working in some coordinate system which may not aligned to the direction of the force and acceleration. To avoid continually changing coordinate systems, instead we can represent newtons second law in terms of vectors.
So the equation becomes:
![]() =m
=m![]()
Where: m is a scalar and ![]() ,
,![]() are vectors (vectors indicated by the arrow above).
are vectors (vectors indicated by the arrow above).
An alternative notation is to
|
= m |
|
When multiplying a vector by a scalar just multiply each term in the vector by the scalar as follows:
| m |
|
= |
|
So what we are saying is that mass acts proportionally the same in each dimension equally.
We don't need to use matrix notation for this, but if we want to use matrix notation for other reasons, we can easily do so as follows:
|
= |
|
|
Although the real world has 3 dimensions (in Newtonian terms at least) we may be limiting motion to 2 dimensions, for example a snooker table (well that's not quite true, but you know what I mean, can you think of a better example?). So if we are working in two dimensions we only need to use 2 dimensional vectors.
Relative and Absolute Quantities
Some quantities are always relative, that is, in order to measure them you have to choose some arbitrary zero point. Other quantities, such as acceleration are absolute because we are not free to choose the zero value, if our frame of reference is accelerating then Newtons laws do not apply inside that frame of reference.
| Newtonian Physics | Einstianian Physics | |
| time | relative | relative |
| distance | relative | relative |
| velocity | relative | absolute |
| acceleration | absolute | absolute |
Frame-of-reference.
A frame-of-reference is like an orientation for our coordinate system. We can choose to observe and measure are quantities in any Cartesian coordinate system provided that the axes are mutually perpendicular. One frame-of-reference may be moving relative to another.
For example, we could measure the movement of a person walking in a train, in the frame-of-reference of the train or in the frame-of-reference of the earth, or in the frame-of-reference of some completely different object moving on the surface of the earth.
It turns out that Newtons laws are obeyed, regardless of the frame-of-reference that we are observing from, provided that:
- We are consistent, we cant mix say the velocity measures in one frame-of-reference with acceleration measured in another frame-of-reference without taking this into account.
- Newtons laws don't necessarily apply when observed from a rotating frame-of-reference, for example a stationary object with no forces acting on it may appear to be orbiting around a rotating frame-of-reference.
- The two frames of reference are not accelerating relative to each other.
So when we go on to discuss rotation, we have to be very careful about this.
In the programming structure below, a change of frame-of-reference is held in a 'transform' structure.
We may have a hierarchy of nested frames-of-reference, in the example above, the earth is moving relative to the sun, the sun is moving relative... and so on.
In these nested frames-of reference, it may help simplify problems if we can develop rules to allow us to translate quantities up and down the hierarchy as follows:
Mass - changing frame-of-reference
The mass should not change when viewed in different frames of reference
Force - changing frame-of-reference
The force should not change provided that the two frames-of-reference are not moving relative to each other, or if they are moving, that they are moving with a constant relative linear velocity. If the frame of reference is accelerating, then the force needs to be recalculated from the sum of the objects local acceleration and the acceleration of the local frame-of-reference. Then multiply this combined acceleration by the mass.
F absolute =Fl + F' = m * al + m * ar
| where: | |||
symbol |
description |
type |
units |
| Fl | Force in local coordinates. | vector | kg m/s2 |
| F' | additional force component due to acceleration of frame-of-reference. | vector | kg m/s2 |
| m | mass | scalar | kg |
| al | acceleration in local coordinates. | vector | m/s2 |
| ar | acceleration of frame-of-reference. | vector | m/s2 |
Acceleration - changing frame-of-reference
The acceleration measured in the frame-of-reference above the local one is the sum of the objects local acceleration and the acceleration of the local frame-of-reference relative to the frame-of-reference above it.
aa = al + ar
Velocity - changing frame-of-reference
The velocity measured in the frame-of-reference above the local one is the sum of the objects local velocity and the velocity of the local frame-of-reference relative to the frame-of-reference above it.
va = vl + vr
Position - changing frame-of-reference
The position measured in the frame-of-reference above the local one is the sum of the objects local position and the position of the local frame-of-reference relative to the frame-of-reference above it.
pa = pl + pr
Programming structure
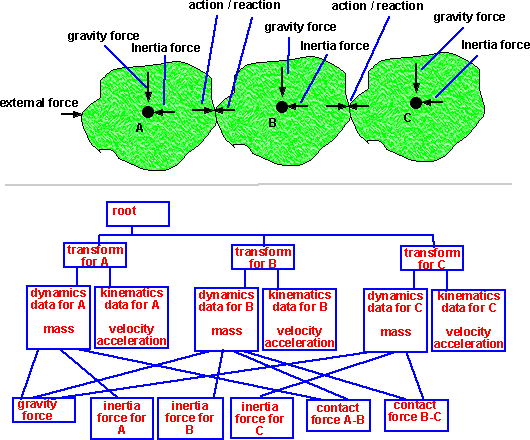
The transform structure holds the relative position of the object, this means that any structures within this can be defined in the local coordinates and inertial frame of the object.
Each object holds its own dynamics data such as mass and kinematics information.
Where should the velocity and acceleration be stored? It seems natural for it to be held in the kinematics data for the object as it is specific to that object. However these quantities are measured in the frame-of-reference above the object (they would be zero relative to itself). So I think it is best to hold it in the kinematics data structure, but to remember that this is relative to the frame-of-reference above it.
From the third law, we know that forces always come in pairs, so we need to hold forces in a separate structure which is associated with two objects. This ensures that the magnitude of the force only needs to be stores once. Strictly gravity should also be associated with two objects, in the same way as the contact forces are, however in the case of gravity the other object is usually the earth, so it is probably more efficient to treat this as a special case. I'm not sure it is necessary to store the inertia force as this can be worked out from m * a, however, it is probably useful to have it when we are doing the calculations so that, in forward dynamics, we can work out all the forces first, then work out the accelerations from that.
For a multiple object simulation such as this then, we might start by looking for an object where the external forces can be determined, in the above example, none of the objects are independent. So we may have to setup a set of equations to determine the inertia force on each object in terms of the forces on the other objects.
What is Force?
This page does not explain what a force is, I'm not sure anyone knows? All we are trying to do is build a mathematical model to define its effects. We cant see a force although, if we become part of the system, we can feel it by pushing against the object. So we can get some intuitive feel for forces, but when we view a system from outside we can't see forces only their effects. So it is just the measurable effects that we are concerned with modelling here.

