This is an example for the page about sheaves which is here.
Theory
| In model theory (see this page) a 'theory' is a set of first-order sentences, for instance: |
|
In this diagram we have a box for each set of these sentances: The arrows mean implies. A set with more sentances can imply a set with less sentances because we are using Intuitionistic logic so we don't use the excluded middle rule. So if a sentance is not included in a set it doesn't mean its false it just means we are not saying anything about it. I have left out arrows if they are given by composing the above arrows. |
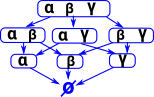 |
| There is more we can imply from these sentances because α and γ implies β so we can add the red arrows: | 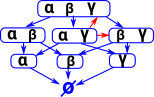 |
| In a similar way we can imply α from β and γ. We can't however imply γ from β and α. | 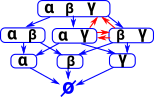 |
| If there is an implication arrow going in both directions we can treat the sets as being the same. So here I have put them in the same box: | 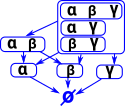 |
We can now draw this as a presheaf.
|
Each entry in set represents a different value for the varable 'y'. We can also have every possible value for the varable 'x' but, to avoid complicating things I have not done this yet. |
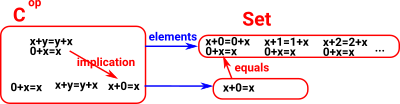 |
Equalities as a Shape
Each equation can be a loop in some space.
What is a 'variable' in a space?
| x=x+0 | <=> | 0=0+0,1=1+0,2=2+0,3=3+0... |
Equalities as a Group or Groupoid
A 'group presentation' represents a group as a set of equations (see page here).
