Cohomology Reversing arrows

One way to introduce cohomology is to start with homology and reverse the arrows. Can we begin with a chain complex consisting of a sequence of matrices and invert these matrices to get a cochain complex?

There are lots of problems with this:

• The matrices are not all square so to find inverse we have to choose left or right inverse if they exist.
• Matrix inverse involves division by determinant, division may not exist in integers so we would have to go to matrix over rationals.
• Determinant of boundary function tends to be zero, see case below.

As an example lets use the chain complex of a flat disk: The determinant of this matrix is zero so we can't invert it.

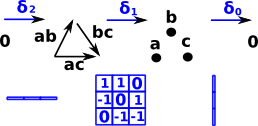So the inverse arrows are not just free groups which can be represented by matrices as with homology.

Reversing the Arrows

In the above diagram the boundary map goes from lines to points for example. each line maps to exactly 2 points.

When we reverse the direction of the boundary map then each point maps to multiple lines.

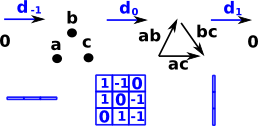So we transpose the matrix rather than invert it.

 

EuclideanSpace

home

Where Are You

This is one of a series of pages about topology, these pages start here.

For other pages, on the site, about topology see:

• Open Sets
• Fibre bundles
• Simplectical Complexes
• Delta Complexes
• Homotopy
• Homology

Computer Code Implementation

I have written some code to implement algebraic topology structures. This is described on the page here and the actual code is on GitHub here.