 |
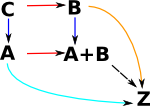
A pushout in category theory is a kind of colimit. This is a generalisation of a sum discussed on page here. It consists of the sum A+B with two arrows into it, one from A and the other from B. For the pushout we add a third object C with arrows into A and B such that the square commutes. It must have a universal property which is: For any other object Z with maps from A and B there must be a unique arrow from A+B to Z. |
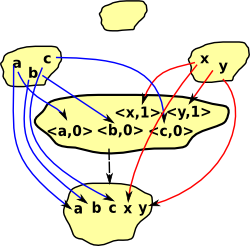
Example in Set
 |
Here we have added set C to the diagram (on the page about sum). Now the square needs to commute. |
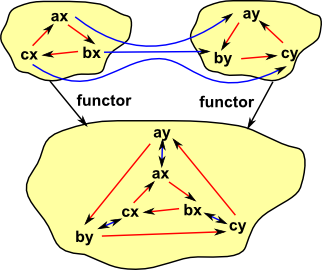
Example in Directed Graph
 |
How does this work when we add structure to the set? For instance, in a directed graph, can we have edges into and out of the intersection? |
Table of Results
Sum |
||
|---|---|---|
| generalisation | a kind of colimit | |
| set example |
|
disjoint union {a,b,c}+{x,y}= |
| group | free product the free product for groups is generated by the set of all letters from a similar "almost disjoint" union where no two elements from different sets are allowed to commute. |
|
| Grp (abelian) | direct sum the group generated by the "almost" disjoint union (disjoint union of all nonzero elements, together with a common zero) |
|
| vector space | direct sum | |
| poset | least upper bound join |
|
| base topological space | wedge | |
| POS |
|
least upper bounds (joins) |
| Rng | ||
| Top | disjoint unions with their disjoint union topologies | |
| Grf | ||
| category |
Sum
When generating a sum for objects with structure then the structure associated with the link can be added to the sum object.