Maths - Multivector Determinant

The determinant in 'n' dimentions is the exterior product of 'n' vectors, this gives the multipier of the pseudoscalar. For instance:

• In 2 dimensions the determinant of 2 vectors is A /\ B which has units of e₁₂
• In 3 dimensions the determinant of 3 vectors is A /\ B /\ C which has units of e₁₂₃
• In 'n' dimensions the determinant of n vectors is A₁ /\ ... A_n which has units of e_1...n

The geometric interpretation of this is shown on this page.

To illustrate this we will start with 2 dimensions:

Two dimensions

Imagine we want to find the directed area enclosed by the parallelogram between two vectors in a plane then we can take the '/\' product:

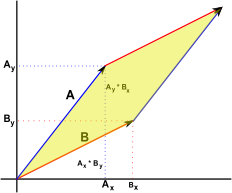
For example if the two vectors are:

2 e₁ + 5 e₂
3 e₁ + 4 e₂

then the directected area is the bivector part of:

(2 e₁ + 5 e₂) /\ (3 e₁ + 4 e₂)

Assuming we are working in euclidean space, that is e₁ and e₂ both square to +1, then we get:

2 e₁ /\ 3 e₁ + 5 e₂ /\ 3 e₁+ 2 e₁ /\ 4 e₂ + 5 e₂ /\ 4 e₂

but the exterior product of common terms is zero: e₁ /\ e₁= e₂ /\ e₂ = 0 so the result is:

(2*4 - 5*3) e₁₂

So the bivector part is 2*4 - 5*3, in matrix notation this is:

2 5 3 4

e12

In the more general case, if we have two vectors (Ax,Ay) and (Bx,By) then the directed area will be (in matrix notation):

Ax Ay Bx By

= A /\ B

Note: we can put the e1 and e2 operators inside this notation: Ax e1 Ay e2 Bx e1 By e2 which expands to give: (Ax e1)(By e2) - (Ay e1)(Bx e2) = (Ax*By - Ay*Bx)e12 Order is important here so the determinant is defined as top-left* bottom-right - bottom-left *top-right

Can this be generalised to 'n' dimensions?

Ax Ay Az Bx By Bz Cx Cy Cz

= Ax

By Bz Cy Cz

- Ay

Bx Bz Cx Cz

+ Az

Bx By Cx Cy

and recursing down to the next level gives:

|M| = Ax By Cz + Ay Bz Cx + Az Bx Cy - Ax Bz Cy - Ay Bx Cz - Az By Cx

A /\ B /\ C = (Ax e₁ + Ay e₂+ Az e₃) /\ (Bx e₁ + By e₂+ Bz e₃) /\ (Cx e₁ + Cy e₂+ Cz e₃)

= (Ax*By e₁₂+ Ax*Bz e₁₃
- Ay*Bx e₁₂ + Ay*Bz e₂₃
+ Az*Bx e₃₁ - Az*By e₂₃) /\ (Cx e₁ + Cy e₂+ Cz e₃)

= ((Ax*By- Ay*Bx) e₁₂+ (Az*Bx-Ax*Bz) e₃₁
+ (Ay*Bz - Az*By) e₂₃)) /\ (Cx e₁ + Cy e₂+ Cz e₃)

= (Ax*By- Ay*Bx)e₁₂ (Cx e₁ + Cy e₂+ Cz e₃)
+ (Az*Bx-Ax*Bz)e₃₁ (Cx e₁ + Cy e₂+ Cz e₃)
+ (Ay*Bz - Az*By) e₂₃)(Cx e₁ + Cy e₂+ Cz e₃)

= (Ax*By- Ay*Bx)Cz e₁₂₃ + (Az*Bx-Ax*Bz)Cy e₃₁₂ + (Ay*Bz - Az*By)Cx e₂₃₁

so the resulting pseudoscalar term is:

Ax*By*Cz- Ay*Bx*Cz + Az*Bx*Cy-Ax*Bz*Cy+ Ay*Bz*Cx - Az*By*Cx

which has the same form as |M| above with a few sign changes, I must have reversed the order somewhere.

EuclideanSpace

home

Prerequisites

• Geometric interpretation of determinant
• Determinant using matrices