Maths - Clifford Algebra - Multipication Types

Maths - Multivector Multiplication Types

Here I have tabulated the algebraic rules for the various Grassmann and Clifford vector and scalar multiplications. This allows us to work out higher order products. Therefore any term can be calculated by recursively applying these rules.

	A /\ B	A \/ B	lc(A,B)	rc(A,B)	A * B
vector product	A /\ B (A ≠ B) 0 (A = B)	bil(A,B)	bil(A,B)	bil(A,B)	(A /\ B)+bil(A,B)
commute	B /\ A == - A /\ B	B \/ A == bil^t(A,B)	lc(A,B) == bil^t(A,B)	rc(A,B) == bil^t(A,B)	-(A /\ B)+bil^t(A,B)
common factors	eij /\ eik == 0	eij \/ eik == e1 \/ eijk	lc(eij,eik) == lc(e1,eijk)	rc(eij,eik) == rc(e1,eijk)	eij * eik ==
non-common factors	eij /\ ekm == eijkm	eij \/ ekm == 0	lc(eij,ekm) == 0	rc(eij,ekm) == 0	eij * ekm == eijkm
square	A /\ A == 0 a /\ a == a²	A \/ A == bil(A,A) a \/ a == 0	lc(A,A) == bil(A,A) lc(a,a) == 0	rc(A,A) == bil(A,A) rc(a,a) == 0	AA==bil(A,A) a a == a²
interaction with scalar	a /\ A == aA	a /\ A == 0	lc(a,A) == aA lc(A,a) == 0	rc(a,A) == 0 rc(A,a) == aA	a * A == aA
scalar distribution	a(A /\ B) == (aA) /\ B A /\ (aB)	a(A \/ B) == a bil(A,B)	a(A \/ B) == a bil(A,B)	a(A \/ B) == a bil(A,B)	a(A * B) == (aA) * B A * (aB)
exterior distribution	A /\ (B /\ C) == A/\B/\C	A /\ (B \/ C)	A /\ lc(B,C)	A /\ rc(B,C)	A /\ (B * C)
unit element	1 (scalar) 1 /\ A = A	pseudoscalar pseudo \/ A = A	left: 1 right: pseudoscalar	left: pseudoscalar right: 1	1 (scalar) 1 * A = A
geometric interpretation	part with no common factors union (exclusive-or) join	part with common factors intersection meet
associative	yes	yes	no	no	yes
grade	grade(A /\ B) == 2	grade(A \/ B) ==	grade(lc(A,B)) ==	grade(rc(A,B)) ==	grade(A * B) ==

where:

a,b... = scalars (grade 0)
A,B... = vectors (grade 1)
bil(A,B) = bilinear represented by a (not necessarily diagonally symmetrical) square matrix
bil^t(A,B) = bilinear represented by transpose of square matrix above
e1,e2... = basis vectors
eij = e1 /\ e2

Common Factor Theorem

(x /\ y) \/ (u /\ v) == (x /\ y /\ v) \/ u - (x /\ y /\ u) \/ v

Duality

reversion ~

	concept	dual
	/\	\/
	grade(A) = m	grade(dual(A)) = n - m
	1	pseudoscalar

where:

n = dimension of vector space

Join and Meet

These are two operations associated with geometric intersection and union of spaces, they are denoted by:

	Symbol	Spaces
Meet	/\	intersection
Join	\/	union U

Confusingly meet and join often use the same symbols '/\' and '\/' as the inner and outer products although the results are slightly different. (some books such as Doran and Lasenby invert this and use \/ for meet and /\ for join so we have to be very careful with terminology and notation).

The mathematical structure of meet and join is an example of a lattice,

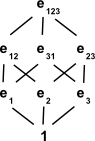
geometric Lattice

Lattices are explained on this page.
Use of lattices for vector subspaces are explained on this page.

A line on this diagram means that the element at the bottom of the line is a direct factor of the element at the top. There is not a line from e1 to e123 because we don't need to include e1 when e1 is already a factor of e12 and e31.

To calculate the meet we take a line upwards from both operands until we get to the lowest common denominator.

Meet /\	1	e1	e2	e3	e12	e31	e23	e123
1	1	e1	e2	e3	e12	e31	e23	e123
e1	e1	e1	e12	e31	e12	e31	e123	e123
e2	e2	e12	e2	e23	e12	e123	e23	e123
e3	e3	e31	e23	e3	e123	e31	e23	e123
e12	e12	e12	e12	e123	e12	e123	e123	e123
e31	e31	e31	e123	e31	e123	e31	e123	e123
e23	e23	e123	e23	e23	e123	e123	e23	e123
e123	e123	e123	e123	e123	e123	e123	e123	e123

To calculate the join we take a line downwards from both operands until we get to the highest common factor.

Join \/	1	e1	e2	e3	e12	e31	e23	e123
1	1	1	1	1	1	1	1	1
e1	1	e1	1	1	e1	e1	1	e1
e2	1	1	e2	1	e2	1	e2	e2
e3	1	1	1	e3	1	e3	e2	e3
e12	1	e1	e2	1	e12	e1	e2	e12
e31	1	e1	1	e3	e1	e31	e3	e31
e23	1	1	e2	e2	e2	e3	e23	e23
e123	1	e1	e2	e3	e12	e31	e23	e123

Bilinear and Quadratic Forms

A quadratic form is an expression in a number of variables where each term is of degree two.

Every quadratic form can be represented by a symmetric matrix, to generate the quadratic form we pre-multiply the matrix by a single row vector containing the variables and post-multiply the matrix by a single column vector also containing the variables.

1	3
3	1

=x² + 6xy + y²

More about bilinear form on this page and quadratic form on this page.

metadata block

see also:

Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.

Clifford Algebra to Geometric Calculus: A Unified Language for Mathematics and Physics (Fundamental Theories of Physics). This book is intended for mathematicians and physicists rather than programmers, it is very theoretical. It covers the algebra and calculus of multivectors of any dimension and is not specific to 3D modelling.

New Foundations for Classical Mechanics (Fundamental Theories of Physics). This is very good on the geometric interpretation of this algebra. It has lots of insights into the mechanics of solid bodies. I still cant work out if the position, velocity, etc. of solid bodies can be represented by a 3D multivector or if 4 or 5D multivectors are required to represent translation and rotation.

Terminology and Notation

Specific to this page here: