Maths - Clifford Algebra - Non-Orthogonal Bases

This page discusses methods to implement the inner products and Clifford products for the more general non-orthogonal basis.

To do this we need a bilinear form in addition to the operands to the multiplications. The bilinear form can be supplied as an n×n square matrix where 'n' is the dimension of the underlining vector space. If the matrix is diagonal (i.e. non-diagonal terms are zero) then the results will be the same as the simpler orthogonal case explained on this page. Since that method is more efficient I suggest using that where the basis vectors are known to be orthogonal.

Inner Product using Poincaré Duality

There are many types of inner product including regressive inner product, the left and right contraction inner products, meet and so on.

When we are dealing with pure vectors (grade 1 multivectors) then these coincide and are easily implemented as a bilinear product, but for other grades, the results of these inner products diverge.

There are different strategies for implementing the higher grade inner products. It would be good to implement the regressive product directly because it has better algebraic properties, it is associative and it has Poincaré duality with the exterior product. So in theory we could implement the regressive inner product using:

A \/ B = (A* /\ B*)*

I think the problem here is that the Poincaré duality involves Clifford multiplication with the pseudoscalar.

A* = A ° I

but to implement Clifford multiplication we need the regressive product so we have a circular requirements dependency. To break out of this we need a way to multiply with the pseudoscalar without the full multiplication. I am not sure how to do this?

Let W be a fixed volume form, i.e. W=e1/\../\en for the generators {ei}_{i=1}^n of V
The volume form spans a one dim space over k, since k is a field we can divide. Define a dual element to A = a1/\../\al  as

A* = a(l+1)/\.../\an, such that  A/\A*=c W with c in k

The meet can now be computed in the dual algebra by using the wedge there !

A=a/\x, B=x/\c, W = a/\b/\c
Let A* = c, B*=a and
A\/B = [A*/\B*]* = [c/\a]* = -(a/\c)* = b, so x=b is the common
factor, which is the intersection point of the two lines A and B

Left and Right Contraction Inner Product

The alternative is to work out the left contraction and use this to calculate the other products

lc (and rc) can be computed recursively (on the basis and then linearly extended)

where:

Let x,y,z.. in V and u,v,w,.. in /\V
Define a left contraction as (I drop the B which should index _| since it will not change here):

i)  x _| y = B(x,y)
   (this relates our bilinear form to the contraction)
ii) x_ (u/\v) = (x_|u)/\v + (-1)^(deg(x)*deg(u)) u/\(x_|v)
     (deg(x)=1, and (-1)^deg(u) gives a sign, this says _| is a graded derivation, Leibniz rule)
iii)  (u/\v) _| w = u _| (v _| w)) left module struture

We are almost there... :-) We can now define (extend) the bilinear form on all Grassmann elements as follows:

< | > : /\V x /\V --> k ::  (A,B) |-->  <A | B > = constant term of(=[1](..) ) (a1/\../\al) _| (b1/\../\bl)
       and zero if A and B have different number of elements ai and bk
(since then no constant term arises) (and extend this linearly to all of /\V x /\V

Example:
<a1/\a2|b1/\b2> = [1]( a1/\a2 _| b1/\b2 ) = [1]( a1_| (a2_| (b1/\b2))
(rule iii)
  = [1]( a1_|( B(a2,b1)b2-B(a2,b2)b1 ))  (rule ii and rule i)
  = [1](B(a1,b2)B(a2,b1) -B(a1,b1)B(a2,b2))   (rule i) which is
already a scalar, so [1] trivial
  = - det [ B(ai,bj) ]
in general you get somthing like (-)^(k(k-1)/2 (?)) det [B(ai,bj)]

This map generalizes the duality V --> V* to /\V --> /\V* ~= (/\V)*

Code

Here is SPAD code for left and right inner products:

Left Contraction Inner Product

Notation: lc and rc (can't use _| because _ is escape character)

Code:

        -- Implement left contraction on individual term in a
        -- multivector and add it to the multivector.
        lcProdTerm(op1mult: K, op1type:SINT, op2mult: K, op2type:SINT): % ==
          resul:% := New
          grade1 := gradeTerm(op1type) -- grade of first operand
          grade2 := gradeTerm(op2type) -- grade of second operand
          if grade1 = 0 then -- 1st operand is scalar so return scalar product
            resul.op2type := resul.op2type + op1mult*op2mult
            return resul
          grade2 = 0 => resul -- 2nd operand is scalar so return 0
          if grade1 = 1 and grade2 = 1 then -- vect _| vect = bilinear
            resul.(0$NNI) := resul.(0$NNI) + op1mult * op2mult * bilinear(op1type,op2type) -- add scalar term
            return resul
          if grade1 = 1 then -- 1st operand is vector so apply: x_|(u^v)=(x_|u)^v - u^(x_|v)
            uType:SINT := leftMostBase(op2type) -- highest ^factor
            vType:SINT := xor(op2type,uType) -- remaining ^factors
            inner2:% := New; inner2.vType := 1$K
            left:% := _/_\(lcProdTerm(op1mult, op1type,op2mult, uType),inner2)
            inner4:% := New; inner4.uType := 1$K
            resul := resul + left + _/_\(inner4,lcProdTerm(-op1mult, op1type,op2mult, vType))
            return resul
          -- if none of the above is true then apply:
          -- (u/\v) _| w = u _| (v _| w)
          uType:SINT := leftMostBase(op1type) -- highest ^factor
          vType:SINT := xor(op1type,uType) -- remaining ^factors
          inner2:% := New
          inner2.uType := 1$K
          resul := resul+ lc(inner2,lcProdTerm(op1mult,vType,op2mult,op2type))
          resul

        -- Implement left contraction inner product
        lc(x:%,y:%): % ==
            z := New
            for ix in 0..dim-1 repeat
                if x.ix ~= 0 then for iy in 0..dim-1 repeat
                    if y.iy ~= 0 then z := z + lcProdTerm(x.ix,ix::SINT,y.iy,iy::SINT)
            z

Right Contraction Inner Product

Notation: lc and rc (can't use _| because _ is escape character)

Code:

        -- Implement right contraction on individual term in a
        -- multivector and add it to the multivector.
        rcProdTerm(op1mult: K, op1type:SINT, op2mult: K, op2type:SINT): % ==
          resul:% := New
          grade1 := gradeTerm(op1type) -- grade of first operand
          grade2 := gradeTerm(op2type) -- grade of second operand
          if grade2 = 0 then -- 1st operand is scalar so return scalar product
            resul.op1type := resul.op1type + op1mult*op2mult
            return resul
          grade1 = 0 => resul -- 2nd operand is scalar so return 0
          if grade1 = 1 and grade2 = 1 then -- vect |_ vect = bilinear
            resul.(0$NNI) := resul.(0$NNI) + op1mult * op2mult * bilinear(op1type,op2type) -- add scalar term
            return resul
          if grade2 = 1 then -- 1st operand is vector so apply: (v^u)|_x=v^(u|_x) - (v|_x)^u
            uType:SINT := rightMostBase(op1type) -- lowest ^factor
            vType:SINT := xor(op1type,uType) -- remaining ^factors
            inner2:% := New; inner2.vType := 1$K
            right:% := _/_\(inner2,rcProdTerm(op1mult, uType,op2mult, op2type))
            inner4:% := New; inner4.uType := 1$K
            resul := resul + _/_\(rcProdTerm(op1mult, vType,-op2mult, op2type),inner4) + right
            return resul
          -- if none of the above is true then apply:
          -- w |_ (v/\u) = (w |_ v) |_ u
          uType:SINT := rightMostBase(op2type) -- lowest ^factor
          vType:SINT := xor(op2type,uType) -- remaining ^factors
          inner2:% := New
          inner2.uType := 1$K
          resul := resul+ rc(rcProdTerm(op1mult,op1type,op2mult,vType),inner2)
          resul

        -- Implement right contraction inner product
        rc(x:%,y:%): % ==
            z := New
            for ix in 0..dim-1 repeat
                if x.ix ~= 0 then for iy in 0..dim-1 repeat
                    if y.iy ~= 0 then z := z + rcProdTerm(x.ix,ix::SINT,y.iy,iy::SINT)
            z

Clifford Product

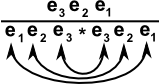
In the orthogonal case we combine the two operands bases into a single word and then shuffle to get the correct result.

The Clifford product may be defined along the lines of lc using the definition

and a similar expansion on the right hand side argument 'u' of cliMul

It is computationally efficient to expand always the smaller element (in terms of its grade (= number of basis vectors))

In this non-orthogonal case we can also shuffle tems from the left operand to the right operand although in a more complicated way:

(ea /\ … /\ eb /\ ec) * (ef /\ … /\ eg ) =
  (ea /\ … /\ eb) * (ec _| (ef /\ … /\ eg) + ec /\ ef /\ … /\ eg ) - (ea /\ … /\ eb |_ ec) * (ef /\ … /\ eg)

from arXiv:math-ph/0212031v1 10 Dec 2002 by Rafal Ablamowicz, B. Fauser.

or in different notation with x,y in V u,v,w in W=/\V we have:

(u /\ x) * v = u * (x _| v + x /\v) - (u |_ x) * v

We also have the following special cases,

  1. x * y = lc(x,y) + x/\y and 1*1=1
  2. x * (u /\ v) = x /\ u /\ v + lc(x, u/\v)
    = x/\u/\v + lc(x,u)/\v + gradeinvolution(u) /\ lc(x, v)
    (same for (u/\v) * y using right contraction)
  3. Since every term u can be recursively be decomposed as a Clifford product
    you can finally evaluate u * v by
    u = w*x (where the grade of w is strictly less than that of u
    u * v = (w*x)*v = w*(x*v) and use the above recursion with 1*1=1

Code for Clifford Product

Here is SPAD code for Clifford product:

        -- Implement Clifford multiplication on individual term in a
        -- multivector and add it to the multivector.
        cliffordProdTerm(op1mult: K, op1type:SINT, op2mult: K, op2type:SINT): % ==
          resul:% := New
          grade1 := gradeTerm(op1type) -- grade of first operand
          grade2 := gradeTerm(op2type) -- grade of second operand
          if grade1 = 0 then -- 1st operand is scalar so return scalar product
            resul.op2type := resul.op2type + op1mult*op2mult
            return resul
          if grade2 = 0 then -- 2nd operand is scalar so return scalar product
            resul.op1type := resul.op1type + op1mult*op2mult
            return resul
          if grade1 = 1 and grade2 = 1 then -- vect * vect = bilinear + x/\y
            resul.(0$NNI) := resul.(0$NNI) + op1mult * op2mult * bilinear(op1type,op2type) -- add scalar term
            resul := resul + exteriorProdTerm(op1mult,op1type,op2mult,op2type) -- add exterior term
            return resul
          if grade1 = 1 then -- 1st operand is vector so apply:
            -- x*(u/\v) = x /\ u /\ v + x _| (u/\v)
            -- = x/\u/\v + (x_|u)/\v + gradeinvolution(u) /\ (x _| v)
            uType:SINT := leftMostBase(op2type) -- highest ^factor
            vType:SINT := xor(op2type,uType) -- remaining ^factors
            xt:% := New; xt.op1type := 1$K
            ut:% := New; ut.uType := 1$K
            vt:% := New; vt.vType := 1$K
            resul := _/_\(xt,exteriorProdTerm(1$K,uType,1$K,vType)) -- x/\u/\v
            resul := resul +  _/_\(lcProdTerm(1$K,op1type,1$K,uType),vt) -- (x _| u)/\v
            resul := resul +  _/_\(gradeInvolutionTerm(1$K,uType),lcProdTerm(1$K,op1type,1$K,vType)) -- gradeinvolution(u) /\ (x _| v)
            resul := (op1mult*op2mult)*resul -- apply 'scalar' multipliers
            return resul
          if grade2 = 1 then -- 2nd operand is vector so apply:
            -- (v/\u)*x = v /\ u /\ x + rc(v/\u,x)
            -- = v/\u/\x + v/\rc(u,x) +  rc(u, x)/\ gradeinvolution(v)
            uType:SINT := rightMostBase(op1type) -- lowest ^factor
            vType:SINT := xor(op1type,uType) -- remaining ^factors
            xt:% := New; xt.op2type := 1$K
            ut:% := New; ut.uType := 1$K
            vt:% := New; vt.vType := 1$K
            resul := _/_\(exteriorProdTerm(1$K,vType,1$K,uType),xt) -- v/\u/\x
            resul := resul +  _/_\(vt,rcProdTerm(1$K,uType,1$K,op2type)) -- v/\(u |_ x)
            resul := resul +  _/_\(rcProdTerm(1$K,vType,1$K,op2type),gradeInvolutionTerm(1$K,uType)) -- (v |_ x)/\ gradeinvolution(u)
            resul := (op1mult*op2mult)*resul -- apply 'scalar' multipliers
            return resul
          -- if none of the above is true then apply:
          -- u*v = u/\v + \/(u,v)
          -- so,
          -- u/\v = u*v - \/(u,v)
          -- (u/\v)*w = v*v*w - bilinear(u,v)*w
          uType:SINT := leftMostBase(op1type) -- highest ^factor
          vType:SINT := xor(op1type,uType) -- remaining ^factors
          ut:% := New; ut.uType := 1$K
          wt:% := New; wt.op2type := 1$K
          resul := ut * cliffordProdTerm(1$K,vType,1$K,op2type)
          resul := resul - bilinear(uType,vType)*wt
          resul := (op1mult*op2mult)*resul -- apply 'scalar' multipliers
          resul

        x * y ==
            z := New
            for ix in 0..dim-1 repeat
                if x.ix ~= 0 then for iy in 0..dim-1 repeat
                    if y.iy ~= 0 then z := z + cliffordProdTerm(x.ix,ix::SINT,y.iy,iy::SINT)
            z

Inverse Multiplication

Grade involution

In mathematics an involution is a function f that is its own inverse. In this case multiplication of a vector by -1. If we invert the vector space then what effect does this have on the higher order basis?

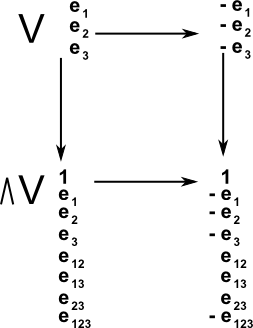grade involution

So grade 1 is inverted but grade 2 is not inverted since the two -1's cancel out. So the pattern is:

grade=g -1g
0 (scalar) 1
1 (vector) -1
2 (bivector) 1
3 -1
4 1

 

When we apply an involution to a multivector then we invert each term seperately according to its grade: multiplier = -1g

Any (Grassmann-) Clifford algebra is built up from a base space V (of dimension dim V = n) You have two natural transformations on V which generalize to the whole space W=/\V of dim W = 2n.

  1. The identity map (does nothing on W)
  2. The map sending every vector v \in V to its additiove inverse (negative)
    barV : V -> V :: v |--> -v
    This will send any basis vector to its negative (regardless of the bilinear form). So iff your basis is like the grBasis :=[Id, e1, e2, e1we2, e3,...]
    barW will send all elements eiw..wej to (-1)number of basis elementseiw..wej
  3. Iff the basis is more general (like in the case with an antisymmetric part in the bilinear form, you always find a new basis (inhomgeous in the old generators) such that the involution does the trick for the new basis elements.

Eg: B:= matrix [[1,q],[-q ,1]] you would like to define a new Grassmann basis

grBasWf = [Id, f1(=e1),f2(=e2), f1wf2 ( f1wf2-q*Id), f3 (=e3),...] etc

In this case you will see that the new basis is graded (only even or odd elements appear) so the involution still works as expected.

What you technically do is the following:

  • Take a vector space V
  • build the free algebra over it, that is the tensor algebra TV, its product is concatenation it is noncommutative
  • You are only intersted in antisymmetric tensors, hence factor out all symmetric ones. That is you identify all terms of the form
    (v1 (x)... (x) vi (x) vi (x) ... (x) vd) = 0

[One can check that this is a graded ideal I_gr and one can therefore factor the tensor algebra TV/I_gr = /\V
(for the generators this means you impose ei^2=0. From that you conclude that
0=(ei+ej)^(x)2 = ei^2+ei (x) ej + ej (x) ei + ej^2
= ei (x) ej + ej (x) ej
calling the projectet tensor /\ you get
ei /\ ej = - ej /\ ei )

Reversion

We can find the multipicative inverse of a single blade by multiplying numerator and denominator by the reverse, that is the bases are written down in the reverse order, the denominator will then collapes down to a scalar value.

reversion

Clifford Basis

A multivector based on two dimensional vectors can be:

a + b e1 + c e2 + d e1/\e2

A Clifford basis is:

a' + b' e1 + c' e2 + d' e1*e2
a' + d' B(e1,e2) + b' e1 + c' e2 + d' e1/\e2

Reversal

in Grassmann basis:

reverse(e1/\e2) = e2/\e1 = - e1/\e2

in Clifford basis:

reverse(e1* e2) = e2 * e1= e2 /\ e1+ B(e2 , e1)= - e1 /\ e2+ B(e2 , e1)

The reversion needs to know about the Clifford multiplication, so its actually defined in the Clifford basis

cliBas:= [Id, e(1), e(2), e(12):=e(1)*e(2), e(3),... ]

and it reverses the order of the Clifford multiplication (which depends on the quadratic (bilinear) form. Hence you have (eij) Grassmann , e(ij) Clifford basis elements)
reversion e12 = reversion (e(12)-B(e1,e2)*Id) = e(21)-B(e1,e2)*Id
= e2/\e1 +(B(e2,e1)-B(e1,e2))*Id
= -e12 - 2F(e1,e2)

where F(e1,e2) is the antisymmetric part of B, hence this difficulty will only appear when there is an antisymmetric part. Since not many people have looked at that, its rarely described in literature, but see B. Fauser, Rafal Ablamowicz:

  • Mathematics of CLIFFORD - A Maple package for Clifford and Grassmann algebras
    Rafal Ablamowicz, B. Fauser: Adv. in Appl. Clifford Alg. 15 No. 2, 2005:157-181
  • arXiv:math-ph/0212032
    Clifford and Grassmann Hopf algebras via the BIGEBRA package for Maple
    Rafal Ablamowicz, B. Fauser: Comp. Physics Comm. 170, 2005:115--130
    available from the arXiv.

Technically the reversion comes from the dualising the vector space V -> V* and building the tensor algebra over the dualised vector space V* and identifying V* ~= V canonically. The project onto antisymmetric tensors. You see that the symmetric group acts on tensors by permuting the 'list' ov vectors a tensor is forms of. The reverison is the unique larget permutation (usually called w) with the most inversions (in reduced notation). So reversion is not just adding a sign, its really reversing the list of all vectors (generators) and then reorder them using the antisymmetry and collect the minus signs.

How do we invert a more general multivector (if it is invertable)?

Conjugation

Conjugation is just the composition of reversion and grade involution:

conjugation x == reversion grade involution x
(== gradeinvolution reversion x) -- order does not matter

General Inverse

See this article

http://www.ceac.aston.ac.uk/research/staff/jpf/papers/paper24/index.php

metadata block
see also:

 
Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.
flag flag flag flag flag flag Clifford Algebra to Geometric Calculus: A Unified Language for Mathematics and Physics (Fundamental Theories of Physics). This book is intended for mathematicians and physicists rather than programmers, it is very theoretical. It covers the algebra and calculus of multivectors of any dimension and is not specific to 3D modelling.

 

flag flag flag flag flag flag New Foundations for Classical Mechanics (Fundamental Theories of Physics). This is very good on the geometric interpretation of this algebra. It has lots of insights into the mechanics of solid bodies. I still cant work out if the position, velocity, etc. of solid bodies can be represented by a 3D multivector or if 4 or 5D multivectors are required to represent translation and rotation.

 

Terminology and Notation

Specific to this page here:

 

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.