We want to understand a space based on four dimensions, lets assume for now that the 3 space dimensions square to a positive scalar value and the time dimension squares to a negative scalar value.
Since its hard to think in 4 dimensions lets look at the individual basis vectors and their products. In that way we can think in terms of various slices through 4 dimensional space.
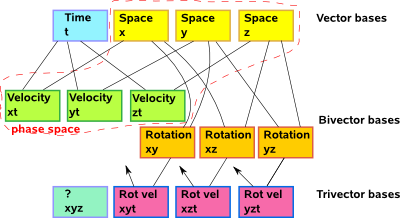
Velocity
Each of the 3 velocity boxes above represents a bivector base which intersect space along the x,y and z dimensions respectively.
If we look at a plane with one space dimension and one time dimension then we see a plane where:
- A point represents an event in space-time.
- A line represents a moving particle and the angle of the line represents the velocity of the particle (along the given dimension).
We looked at transforms in such a plane on this page. There we found that the transforms: translations and rotations can be calculated in using exactly the same procedure:
- Take the exponent of both inputs.
- Multiply these exponents together.
- Take the ln (loge) of the result.
The way we distinguish between translations and rotations is that we use double numbers for one and complex numbers for the other:
| 2D Minkowski space (1 space and 1 time) |
|
|---|---|
| translations | complex numbers |
| rotations | double numbers |
This is the inverse of the space rotation bivectors below, so in the way we combine rotations they behave as we would expect translation to behave in 2 space dimensions and visa versa.
So rotation of a line, which represents a change of velocity, is done using double numbers. This is effectively vector addition which is what we would expect to use to combine velocities.
Translation of a line would not change the path or speed of the particle but it would change when it reaches a given point. This is combined with other translations in the same way as rotations are calculated in conventional space. This seems to imply that movement in space-time has wave-like properties.
We will investigate this further, for say a photon, on this page.
Space Rotation
In 2 space dimensions we can combine translations and rotations using vector and scalar addition respectively. However to be compatible with the other cases we will take the exponent and multiply as follows:
2D Euclidean space |
|
|---|---|
| translations | double numbers |
| rotations | complex numbers |
We can then scale this up to all 3 space dimensions by using quaternions as described here.
Rotational Velocity
This trivector bases are volumes in 4D space, the duals of the base vectors, those containing a time dimension represent angular velocity.
Phase Space
In order to take a snapshot of the state of a system of particles we need to measure the position and velocity of every particle in the system. So for a 3 dimensional classical system this would require:
- A 3 dimentional vector for the position.
- A 3 dimentional vector for the velocity (or momentum).
So altogether it requires 6*n scalar values where n is the number of particles.
If the particles can also have spin (see this page), then we also require a 3 dimensional bivector for that, giving a total of 9*n scalar values.
In special relativity things get a bit more complicated because we cant use the same timestamp for everything.