Physics - Derivation of Inertia Tensor

To derive the expression for the inertia tensor lets calculate the angular velocity due to a torque for a small cube of matter and then integrate this over the whole mass of the object.

However, there is a problem, how do we apply a torque to one point only? I thought of having two small cubes on opposite sides of the centre of mass but this would only work if the object were symmetrical. So instead I will pin the centre of mass to the origin, because this is the centre of mass when we integrate the forces on the origin should cancel out?

So lets start with a torque Tx around the x axis:

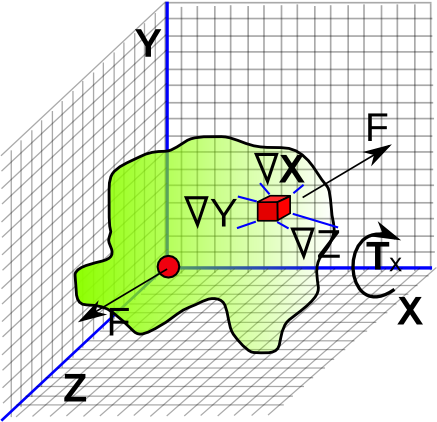
So we take a small volume (Δx,Δy,Δz) at the point (r_x,r_y,r_z) which has the mass Δm

How do we apply a force couple to generate the required torque?

The inertia tensor represents the relationship between the torque and the angular acceleration as follows:

T = [I]α

Or alternativly, the relationship between the angular momentum and the angular velocity, we will use this:

L = angular momentum = [I]ω

we can represent the angular momentum of the small particle as its linear velocity multiplied (cross product) by its distance from the centre of rotation. So integrating over all the particles gives:

L = ∫ r × v dm

but the linear velocity v = ω × r, substituting this gives:

L = ∫ r × (ω × r) dm

We can use this result using geometric algebra or we and convert to the more usual matrix form by replacing these vectors with a screw symmetric matrix as follows:

Matrix Representation

r × (ω × r)

= -r × (r ×ω)

= -[~r][~r]ω

I = - ∫

0 - rz ry rz 0 - rx -ry rx 0

0 - rz ry rz 0 - rx -ry rx 0

dm

I = - ∫

-rz²-ry² rx*ry rx*rz ry*rx -rz²-rx² ry*rz rz*rx rz*ry -rx²-ry²

dm

I =	∫(rz²+ry²)dm -∫rx*rydm -∫rx*rzdm -∫ry*rxdm ∫(rz²+rx²)dm -∫ry*rzdm -∫rz*rxdm -∫rz*rydm ∫(rx²+ry²)dm

 

EuclideanSpace

home

Transforms