Physics - Rotation of point mass (particle)

On this page we derive the rotation values from a point mass (particle). The point mass is not necessarily rotating about its own axis (although it could, subatomic particles have spin). What we are interested in here is the contribution of the particle to the rotational properties of a bigger mass about some fixed point. If I am not making myself very clear try reading numerical methods.

The following pages will then go on to derive quantities for finite solid bodies by integrating across the volume. Most of these quantities are vectors of dimension 3 which has a component in the x,y and z directions. To denote a vector quantity we show an arrow above the quantity, for more information about vectors see here.

Angular Velocity ()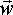

See under kinematics here.

• Angular Velocity of solid body
• Angular Velocity in moving frame-of-reference

Angular Momentum ()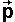

The instantaneous angular momentum of a particle is the product of its mass and its angular velocity.

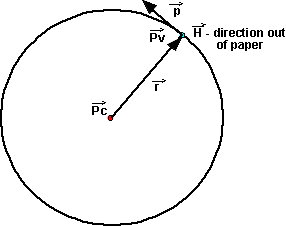
= × = × m =m

where:		other definitions
symbol	description	type	units
	the instantaneous angular momentum about PC	bivector	kg m2/s
×	the cross product operator (see here for definition)
	the instantaneous position of the particle relative to point. -	vector	m
	the instantaneous linear momentum of the particle = m	vector	kg m/s
m	the mass of the particle.	scalar	kg

As with rotation velocity, the angular momentum of a point is not an absolute value, but it depends on which point that the rotation is measured about.

As discussed here, angular momentum of any closed system is conserved. However the particle under consideration here, may have external forces acting on it, so it is not a closed system. When we go on to consider a rigid body rotating about its centre of mass, then the angular momentum of the whole system (about any point) is conserved, this is the sum of the angular momentums of the particles that make up the body. So as it rotates, the instantaneous angular momentum of each particle that makes up the body, will be continuously varying, but the total angular momentum is constant.

• Angular Momentum of solid body
• Angular Momentum in moving frame-of-reference

Angular Acceleration ()

See under kinematics here.

• Angular Acceleration of solid body
• Angular Acceleration in moving frame-of-reference

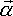Torque ()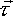

The torque, about point , caused by a force is the cross product of distance from and the force .

= ×

where:		other definitions
symbol	description	type	units
	the instantaneous torque about PC	bivector	N m
	instantaneous position of the particle relative to point. -	vector	m
	instantaneous force on the particle.	vector	N
×	vector cross product operator(see here for definition)

Note that this is both a linear force and a torque about . If we want a 'pure' torque without any net linear force then, we can apply two equal and opposite forces to two particles which are offset. If we want a 'pure' linear force without any net torque, then this will only happen if the torque is measured about the centre of mass of a system of particles, and the force is applied in line with the centre of mass. However on this page we are considering a single particle only, we will go on to consider solid bodies later.

• Torque of solid body
• Torque in moving frame-of-reference

Inertia [I]

We now want to derive the relationship between and .

For, linear motion we have =m from Newtons second law.

It turns out that the equivalent of Newtons second law for rotation is:

= [I]

where:		other definitions
symbol	description	type	units
	the instantaneous torque about PC	bivector	kg m/s2
[I]	moment of inertia	tensor	kg m2
	the instantaneous angular acceleration about PC	bivector	m/s2

But how do we derive this for a particle? and why is the rotational equivalent of the scalar m (mass) a matrix [I]? what are the components of [I] and how are they related to m?

We will try to answer these questions as follows, start with the linear version of Newtons second law:

=m

cross multiply both sides by :

×= × (m)

substituting = × and = ×

gives,

= × ( × m)

It is not easy to combine these two consecutive cross multiplications by because vector are not associative under cross product { x * (y * z) is not (x * y) * z }. however there is a trick which can be done here:

Method using Matrices

The vector cross product can by replaced by matrix multiplication with a skew symmetric matrix as defined below.

So define

[~r] is equivalent to ×

so if:

=

rx ry rz

then:

[~r] =

0 -r3 r2 r3 0 -r1 -r2 r1 0

So applying this to = × ( × m) gives:

=m[~r][~r]

Since matrix multiplication is associative we can calculate [~r][~r] first to give:

EuclideanSpace

home

Screw Theory