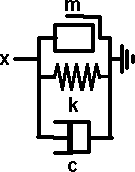
The spring,mass, damper model allows mechanical systems to be solved in is similar way to electrical circuits using capacitors resistors and inductors.
| Spring | Damper | Mass | |
|
Differential equation - Laplace transform -
|
F = k * x F(s) = k * X(s) where k = spring ratio in N/m |
F = c * dx/dt F(s) = c * s * X(s) where c = damping coefficient in N s /m |
F = m * d2x/dt2 F(s) = m * s * s * X(s) where m = mass in kg=N*s*s/m |
Example 1
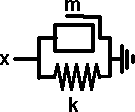
equation of motion: m * d2 x/dt2 + k * x =0
solution x = a * cos(wt + alpha)
where w = sqrt(k / m)
a and alpha are constants of integration
Example 2
equation of motion: m * d2x/dt2 + c *dx/DT + k * x = 0
Standard Components
I think that some components, such as motor, gearbox, rack & pinion, etc. should be available to users as standard building blocks, the internal operation of these would not need to be simulated, only the internal behavior.
Further Information
Example: in car racing game