When converting between Euler angles and other representations of 3D rotations we get singularities. The aim of this page is to give an intuitive understanding of these singularities.
To do this we will compare 3D rotations with a similar, but different, problem - that of representing the surface of the earth on a 2 dimensional plane (Mercator Projection).
This is different because it only involves two angles: latitude and longitude, this should make it more intuitive to understand and yet still illustrate a singularity.
In mathematics there are different types of singularity, in these cases we are talking about the situation where:
- Many points in one representation are mapped onto a single point in another representation.
- Infinitesimal changes close to the singularity in one representation may cause large changes in the other representation.
The Mercator Projection maps the north and south poles to lines this means that, at these points, the projection is many to one:
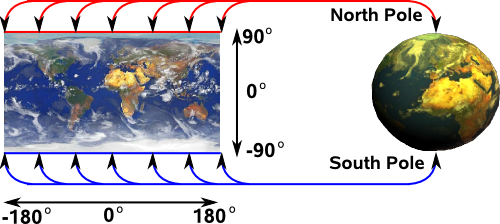
Simarly we can map Euler angles to quaternions (4 dimensional hypersphere). This maps a one dimensional space (rotations around 0,1,0 axis) to a two dimensional plane in Euler terms. This is where attitude = 90° and heading, bank vary:
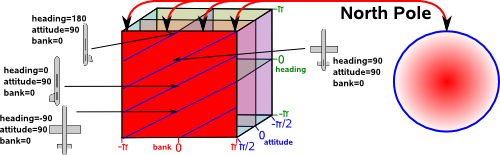
On this plane lines of common orientation are diagonal lines, that is rotation around 0,1,0 axis are given by angle = heading+bank.
Similarly for the south pole.

